题目内容
9.函数y=1+logax(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny-2=0上,其中mn>0,则$\frac{1}{m}+\frac{3}{n}$的最小值为( )
| A. | 2+$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
分析 求出定点A的坐标,代入直线方程,得到m.n的关系,利用基本不等式求解最小值即可.
解答 解:函数y=1+logax(a>0,a≠1)的图象恒过定点A(1,1),若点A在直线mx+ny-2=0上,
可得m+n=2,
$\frac{1}{m}+\frac{3}{n}$=$\frac{1}{2}(\frac{1}{m}+\frac{3}{n})(m+n)$=$\frac{1}{2}$$(1+3+\frac{n}{m}+\frac{3m}{n})$=$2+\frac{n}{2m}+\frac{3m}{2n}$≥2+2$\sqrt{\frac{n}{2m}•\frac{3m}{2n}}$=2+$\sqrt{3}$.
当且仅当m=$\sqrt{3}-1$,n=$3-\sqrt{3}$时取等号.
表达式的最小值为:2+$\sqrt{3}$.
故选:A.
点评 本题考查指数函数的单调性与特殊点的应用,基本不等式的应用,考查计算能力.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
19.下列说法正确的是( )
| A. | 命题“?x∈R使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0” | |
| B. | “p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | |
| C. | “a>1”是“f(x)=logax(a>0,a≠1)在(0,+∞)上为增函数”的充要条件 | |
| D. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”,则¬p是真命题 |
4.已知函数f(x)对任意的x∈R都满足f(x)+f(-x)=0,当x≥0时,f(x)=$\left\{\begin{array}{l}{-x,0≤x≤a}\\{-a,a<x<2a}\\{x-3a,x≥2a}\end{array}\right.$,(a>0),若对?x∈R,都有f(x-2)≤f(x),则实数a的取值范围为( )
| A. | (0,$\frac{1}{4}$) | B. | [$\frac{1}{4}$,$\frac{1}{3}$] | C. | (0,$\frac{1}{3}$] | D. | (0,$\frac{1}{3}$) |
14.若集合A={x|x=in,n∈N+}(i是虚数单位),B={1,-1},则A∩B等于( )
| A. | {-1} | B. | {1} | C. | ∅ | D. | {1,-1} |
1.要得到函数g(x)=$sin(2x+\frac{π}{6})$,只需将f(x)=cos2x的图象( )
| A. | 左移$\frac{π}{3}$个单位 | B. | 右移$\frac{π}{3}$个单位 | C. | 左移$\frac{π}{6}$个单位 | D. | 右移$\frac{π}{6}$个单位 |
19.如图所示是某一几何体的三视图,则这个几何体是( )
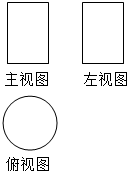

| A. | 圆柱体 | B. | 圆锥体 | C. | 正方体 | D. | 球体 |