题目内容
13．已知p：?x∈R，x2-x+1＞0，q：?x∈（0，+∞），sinx＞1，则下列命题为真命题的是（ ）| A． | p∧q | B． | ￢p∨q | C． | p∨￢q | D． | ￢p∧￢q |
分析 分别判断出p，q的真假，从而判断出其复合命题的真假即可．
解答 解：关于p：?x∈R，x2-x+1=${（x-\frac{1}{2}）}^{2}$+$\frac{3}{4}$＞0，成立，
故命题p是真命题，
关于q：?x∈（0，+∞），sinx＞1，
∵?x∈（0，+∞），sinx≤1，
故命题q是假命题，
故p∨￢q是真命题，
故选：C．
点评 本题考查了二次函数、三角函数的性质，考查复合命题的判断，是一道基础题．
练习册系列答案
相关题目
3．已知复数$\frac{3+i}{x-i}$（x∈R）在复平面内对应的点位于以原点O为圆心，以$\sqrt{2}$为半径的圆周上，则x的值为（ ）
| A． | 2 | B． | 1+3i | C． | ±2 | D． | $±\frac{1}{2}$ |
8．
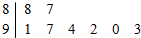若某市8所中学参加中学生比赛的得分用茎叶图表示（如图）其中茎为十位数，叶为个位数，则这组数据的平均数和方差分别是（ ）
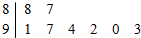若某市8所中学参加中学生比赛的得分用茎叶图表示（如图）其中茎为十位数，叶为个位数，则这组数据的平均数和方差分别是（ ）| A． | 91.5、5 | B． | 91、5 | C． | 92、5.5 | D． | 92、5 |
2．下列函数中，是偶函数且在区间（0，+∞）上是减函数的是（ ）
| A． | $f（x）=\frac{1}{x^2}$ | B． | f（x）=x2 | C． | $f（x）=\frac{1}{x}$ | D． | f（x）=lnx |