16．等比数列{an}中.a1=2.a3=8.则S4=-10或30．——青夏教育精英家教网——

16．等比数列{a_n}中，a₁=2，a₃=8，则S₄=-10或30．

15．函数f（x）=（x+a）²是偶函数的充要条件是a=0．

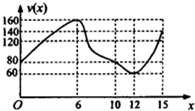一辆赛车在跑道上高速行驶，如图反映了它从某时刻开始的15分钟内速度v（x）与时间x的关系，若定义“速度差函数”u（x）为时间段[0，x]内的最大速度与最小速度的差，则u（x）的图象可能是（　　）

	A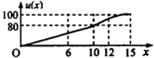．			B．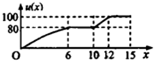
	C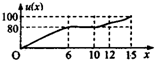．			D．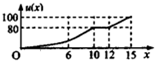

13．设向量$\overrightarrow{a}$=（1，1），i是虚数单位，复数（m-i）•i所对应的向量为$\overrightarrow{b}$，若$\overrightarrow{a}⊥\overrightarrow{b}$，则实数m的值等于（　　）

12．有1000个形状相同的球，其中红球500个，黄球300个，绿球200个，采用按颜色分层抽样的方法随机抽取100个球进行分析，则应抽取红球的个数为（　　）

11．一个几何体的主视图和左视图是两个边长为2的等边三角形，俯视图是直径为2的圆及其圆心，则该几何体的侧面积为（　　）

$\frac{2π}{3}$

10．已知集合A={x|x＞1}，B={x|x＜3}，则集合A∩B=（　　）

9．某种鲜花进价每束2.5元，售价每束5元，若卖不出，则以每束1.6元的价格处理掉，某节日鲜花的需求量X（单位：束）的分布列为

X	200	300	400	500
P	0.20	0.35	0.30	0.15

（Ⅰ）若进鲜花400束，是写出销售量S（单位：束）的分布列，并求利润Y的均值．
（Ⅱ）若进鲜花n束（300＜n≤500），求n取何值时可使利润Y的均值最大？

8．设函数f（x）=$\frac{2\sqrt{3}sin（x+\frac{π}{3}）+6{x}^{2}+\sqrt{3}x}{6{x}^{2}+3cosx}$的最大值为M，最小值为N，则（　　）

7．已知O是坐标原点，点A（-2，2），若点B（x，y）为平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$上一动点，则$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围是[0，4]．

0 250254 250262 250268 250272 250278 250280 250284 250290 250292 250298 250304 250308 250310 250314 250320 250322 250328 250332 250334 250338 250340 250344 250346 250348 250349 250350 250352 250353 250354 250356 250358 250362 250364 250368 250370 250374 250380 250382 250388 250392 250394 250398 250404 250410 250412 250418 250422 250424 250430 250434 250440 250448 266669