题目内容
8.设函数f(x)=$\frac{2\sqrt{3}sin(x+\frac{π}{3})+6{x}^{2}+\sqrt{3}x}{6{x}^{2}+3cosx}$的最大值为M,最小值为N,则( )| A. | M-N=4 | B. | M+N=4 | C. | M-N=2 | D. | M+N=2 |
分析 利用分式函数的性质进行分解,结合奇函数的对称性即可得到结论.
解答 解:函数f(x)=$\frac{2\sqrt{3}sin(x+\frac{π}{3})+6{x}^{2}+\sqrt{3}x}{6{x}^{2}+3cosx}$=$\frac{2\sqrt{3}(sinx•\frac{1}{2}+cosx•\frac{\sqrt{3}}{2})+{6x}^{2}+\sqrt{3}x}{{6x}^{2}+3cosx}$
=$\frac{\sqrt{3}sinx+\sqrt{3}x}{{6x}^{2}+3cosx}$+$\frac{3cosx+{6x}^{2}}{{6x}^{2}+3cosx}$═$\frac{\sqrt{3}sinx+\sqrt{3}x}{{6x}^{2}+3cosx}$+1,
令g(x)=$\frac{\sqrt{3}sinx+\sqrt{3}x}{{6x}^{2}+3cosx}$,则f(x)=g(x)+1.
显然,g(x)为奇函数,且g(x)的最大值为M-1,最小值为N-1,
故M-1+N-1=0,∴M+N=2,
故选:D.
点评 本题主要考查函数最值的判断,利用分式函数进行分解,利用奇函数的最值互为相反数,即可得到结论,属于中档题.

练习册系列答案
相关题目
 某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.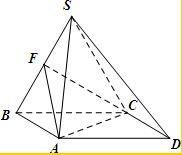 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2$\sqrt{2}$,SB=SC=AB=2,F为线段SB的中点.
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2$\sqrt{2}$,SB=SC=AB=2,F为线段SB的中点.