题目内容
7.已知O是坐标原点,点A(-2,2),若点B(x,y)为平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$上一动点,则$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围是[0,4].分析 先画出满足约束条件的平面区域,求出平面区域的角点后,逐一代入$\overrightarrow{OA}$•$\overrightarrow{OB}$分析比较后,即可得到$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围.
解答 解:满足约束条件的平面区域如下图所示: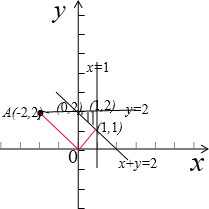 ,
,
将平面区域的三个顶点坐标分别代入平面向量数量积公式
当x=1,y=1时,$\overrightarrow{OA}•\overrightarrow{OB}$=-2×1+2×1=0,
当x=1,y=2时,$\overrightarrow{OA}•\overrightarrow{OB}$=-2×1+2×2=2,
当x=0,y=2时,$\overrightarrow{OA}•\overrightarrow{OB}$=-2×0+2×2=4,
故$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围为[0,4],
故答案为:[0,4].
点评 本题考查的知识点是线性规划的简单应用,其中画出满足条件的平面区域,并将三个角点的坐标分别代入平面向量数量积公式,进而判断出结果是解答本题的关键.

练习册系列答案
相关题目
17.若tanθ=2,则sin2θ+sinθcosθ-2cos2θ=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | $\frac{3}{4}$ |
12.有1000个形状相同的球,其中红球500个,黄球300个,绿球200个,采用按颜色分层抽样的方法随机抽取100个球进行分析,则应抽取红球的个数为( )
| A. | 20个 | B. | 30个 | C. | 50个 | D. | 100个 |
19.下面说法错误的是( )
| A. | 数乘向量就是一个实数λ与向量$\overrightarrow{a}$的乘积 | |
| B. | λ>0,λ$\overrightarrow{a}$就是把$\overrightarrow{a}$同方向放大或缩小 | |
| C. | λ$\overrightarrow{a}$就是把$\overrightarrow{a}$沿反方向放大或缩小 | |
| D. | λ=0,则$λ\overrightarrow{a}$=$\overrightarrow{0}$ |
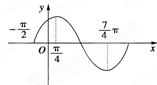 函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的图象如图所示.试求:
函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的图象如图所示.试求: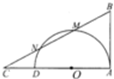 如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.
如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.