题目内容
9.某种鲜花进价每束2.5元,售价每束5元,若卖不出,则以每束1.6元的价格处理掉,某节日鲜花的需求量X(单位:束)的分布列为| X | 200 | 300 | 400 | 500 |
| P | 0.20 | 0.35 | 0.30 | 0.15 |
(Ⅱ)若进鲜花n束(300<n≤500),求n取何值时可使利润Y的均值最大?
分析 (1)由销售量S(单位:束)的分布列求出E(S),再由已知函数求出求出利润Y关于销售量S的函数,由此能求出E(Y).
(2)分别求出当400<n≤500和当300<n≤400时,销售量S(单位:束)的分布列、E(S)、E(Y),由此能得到n取何值时可使利润Y的均值最大.
解答 解:(1)∵销售量S(单位:束)的分布列为:
| S | 200 | 300 | 400 |
| P | 0.20 | 0.35 | 0.45 |
而利润Y=(5-2.5)S-(2.5-1.6)(400-S)=3.4S-360,
∴E(Y)=3.4E(S)-360=3.4×325-360=745.…(6分)
(2)当400<n≤500时,销售量S(单位:束)的分布列为
| S | 200 | 300 | 400 | n |
| P | 0.20 | 0.35 | 0.30 | 0.15 |
∴E(Y)=3.4E(S)-0.9n=-3.9n+901; …(8分)
当300<n≤400时,销售量S(单位:束)的分布列为
| S | 200 | 300 | n |
| P | 0.20 | 0.35 | 0.45 |
E(Y)=3.4E(S)-0.9n=0.63n+493,…(10分)
E(Y)=$\left\{\begin{array}{l}{0.63n+493(300<n≤400)}\\{-0.39n+901(400<n≤500)}\end{array}\right.$,
∴n=400时,E(Y)取最大值745.…(12分)
点评 本题考查离散型随机变量的分布列和数学期望的求法及应用,是中档题,解题时要认真审题,注意分布列的性质的合理运用.

练习册系列答案
相关题目
4.设集合M={x|2x2-x-6<0},N={x|0<x≤4},则M∩N等于( )
| A. | (0,2) | B. | (-$\frac{3}{2}$,0) | C. | (-2,3) | D. | (-2,2) |
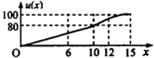
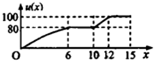
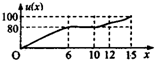
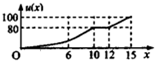
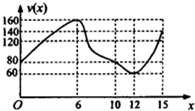 一辆赛车在跑道上高速行驶,如图反映了它从某时刻开始的15分钟内速度v(x)与时间x的关系,若定义“速度差函数”u(x)为时间段[0,x]内的最大速度与最小速度的差,则u(x)的图象可能是( )
一辆赛车在跑道上高速行驶,如图反映了它从某时刻开始的15分钟内速度v(x)与时间x的关系,若定义“速度差函数”u(x)为时间段[0,x]内的最大速度与最小速度的差,则u(x)的图象可能是( )