9.设x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x+y-5≥0}\\{2x-y-3≤0}\end{array}\right.$,若使函数Z=ax+by(2b>a>0)的最大值为10,求ab的最大值( )
| A. | $\frac{25}{7}$ | B. | $\frac{5}{7}$ | C. | 5 | D. | 25 |
8.z=$\frac{{{{({-1+\sqrt{3}i})}^3}}}{2^3}+\frac{{-1+\sqrt{2}i}}{{\sqrt{2}+i}}$,则|z|=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 1 |
7.若f(x),g(x)分别是R上的奇函数和偶函数,则f(x)g(x)一定是( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
5.某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.
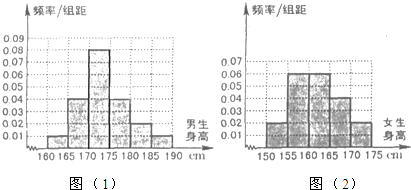
(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
参考数据:

(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
参考数据:
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
3.设实数x,y满足$\left\{\begin{array}{l}{(2x-y+2)(4x-y-2)≤0}\\{0≤x≤2}\\{y≥0}\end{array}\right.$,若目标函数z=mnx+y(0<n<m)的最大值为10,则2m+n的取值范围为( )
| A. | (4,+∞) | B. | [4,+∞) | C. | [3$\sqrt{2}$,+∞) | D. | (3$\sqrt{2}$,+∞) |
2.函数f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是( )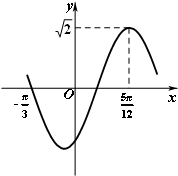
0 248415 248423 248429 248433 248439 248441 248445 248451 248453 248459 248465 248469 248471 248475 248481 248483 248489 248493 248495 248499 248501 248505 248507 248509 248510 248511 248513 248514 248515 248517 248519 248523 248525 248529 248531 248535 248541 248543 248549 248553 248555 248559 248565 248571 248573 248579 248583 248585 248591 248595 248601 248609 266669

| A. | -$\frac{\sqrt{6}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |