题目内容
2.函数f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是( )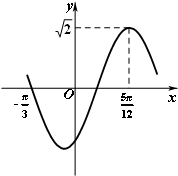
| A. | -$\frac{\sqrt{6}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
分析 由函数的图象可得 $\frac{3}{4}$T,代入周期公式求得ω的值,再由五点作图的第二点列式求得φ的值,即可得解.
解答 解:由图知$\frac{3}{4}$T=$\frac{5π}{12}$-(-$\frac{π}{3}$)=$\frac{3}{4}$π,
∴T=π,即$\frac{2π}{ω}$=π,解得:ω=2.
由五点作图的第二点可知,2×$\frac{5π}{12}$+φ=$\frac{π}{2}$,即φ=-$\frac{π}{3}$,满足|φ|<$\frac{π}{2}$,
∴ω,φ的值分别是2,-$\frac{π}{3}$.
∴f(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$),
∴f(0)=$\sqrt{2}$sin(-$\frac{π}{3}$)=-$\frac{\sqrt{6}}{2}$.
故选:A.
点评 本题考查由y=Asin(ωx+φ)的部分图象求解函数解析式,解答的关键是由五点作图的某一点列式求解φ的值,是基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
13.若复数$\frac{3-ai}{1+2i}$(i为虚数单位,a∈R)在复平面内对应点在第四象限,则a的取值范围为( )
| A. | {a|a<-6} | B. | $\left\{{a|-6<a<\frac{3}{2}}\right\}$ | C. | $\left\{{a|a<\frac{3}{2}}\right\}$ | D. | $\left\{{a|a<-6或a>\frac{3}{2}}\right\}$ |
10.在等比数列{an}中,若a4,a8是方程x2-4x+3=0的两根,则a6的值是( )
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{3}$或-$\sqrt{3}$ | D. | ±3 |
7.若f(x),g(x)分别是R上的奇函数和偶函数,则f(x)g(x)一定是( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
14.已知三点坐标分别为:A(-1,-1),B(1,3),C(2,x),且满足三点共线,则x=( )
| A. | 5 | B. | -5 | C. | 4 | D. | -4 |
11.一个礼堂有4个门,若从任一门进,从任一门出,共有不同的走法( )
| A. | 8种 | B. | 12种 | C. | 16种 | D. | 24种 |
12.某班40个学生平均分成两组,两组学生某次考试的成绩情况如下表所示:
求这次考试全班的平均成绩和标准差.( 注:平均数$\overline{x}=\frac{{{x_1}+{x_2}+…+{x_n}}}{n}$,
标准差$s=\sqrt{\frac{1}{n}[{({x_1}-{{\overline{x)}}^2}+{{({x_2}-\bar\overline{x})}^2}+…+{{({x_n}-\bar\overline{x})}^2}}]}=\sqrt{\frac{1}{n}[{(x_1^2+x_2^2+…+x_n^2)-n{{\bar\overline{x}}^2}}]}$)
| 组别 | 平均数 | 标准差 |
| 第一组 | 90 | 4 |
| 第二组 | 80 | 6 |
标准差$s=\sqrt{\frac{1}{n}[{({x_1}-{{\overline{x)}}^2}+{{({x_2}-\bar\overline{x})}^2}+…+{{({x_n}-\bar\overline{x})}^2}}]}=\sqrt{\frac{1}{n}[{(x_1^2+x_2^2+…+x_n^2)-n{{\bar\overline{x}}^2}}]}$)