Question

9．设x，y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x+y-5≥0}\\{2x-y-3≤0}\end{array}\right.$，若使函数Z=ax+by（2b＞a＞0）的最大值为10，求ab的最大值（　　）

• A． $\frac{25}{7}$
• B． $\frac{5}{7}$
• C． 5
• D． 25

Answer 1

分析 先画出满足条件的平面区域，由Z=ax+by（2b＞a＞0）得：y=-$\frac{a}{b}$x+$\frac{z}{b}$，由图象显然直线过A点时取得最大值，得到5a+7b=10，利用基本不等式的性质解出即可．

解答 解：画出满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x+y-5≥0}\\{2x-y-3≤0}\end{array}\right.$的平面区域，如图示：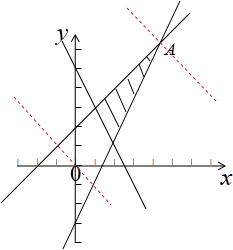
，
由Z=ax+by（2b＞a＞0）得：y=-$\frac{a}{b}$x+$\frac{z}{b}$，
显然直线过A点时取得最大值，
由$\left\{\begin{array}{l}{x-y+2=0}\\{2x-y-3=0}\end{array}\right.$，解得：A（5，7），
∴z=5a+7b=10，
∴5a+7b=10≥2$\sqrt{5a•7b}$，
∴35ab≤25，∴ab≤$\frac{5}{7}$，
故选：B．

点评 本题考查了简单的线性规划问题，考查基本不等式的性质，数形结合思想，是一道中档题．