3.执行如图所示的程序框图,若输出的结果是27,则输入的数是( )
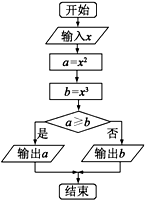

| A. | -3或-3$\sqrt{3}$ | B. | 3或-3$\sqrt{3}$ | C. | -3或3$\sqrt{3}$ | D. | 3或3$\sqrt{3}$ |
2.随着移动互联网的深入普及,用手机上网的人数日益增多,某教育部门成立了调查小组,调查“常上网与高度近视的关系”,对某校高中二年级800名学生进行检查,得到如下2×2列联表:
根据列联表的数据,计算得到K2≈7.524,则( )
| 不常上网 | 常上网 | 总计 | |
| 不高度近视 | 70 | 150 | 220 |
| 高度近视 | 130 | 450 | 580 |
| 总计 | 200 | 600 | 800 |
| A. | 有99.5%的把握认为常上网与高度近视有关 | |
| B. | 有99.5%的把握认为常上网与高度近视无关 | |
| C. | 有99%的把握认为常上网与高度近视有关 | |
| D. | 有99%的把握认为常上网与高度近视无关 |
1.已知函数f(x)的图象是连续不断的,现给出x,f(x)的部分对应值如下表:
则函数f(x)一定有零点的区间是( )
| x | -2 | -1 | 1 | 2 | 3 |
| f(x) | -3 | -2 | 1 | 2 | 4 |
| A. | (1,2) | B. | (2,3) | C. | (-2,-1) | D. | (-1,1) |
19.某校高一年级有200人,其中100人参加数学第二课堂活动.在期末考试中,分别对参加数学第二课堂活动的同学与未参加数学第二课堂活动的同学的数学成绩进行调查.按照学生数学成绩优秀与非优秀人数统计后,构成如下不完整的2×2列联表:
已知p是(1+2x)5展开式中的第三项系数,q是(1+2x)5展开式中的第四项的二项式系数.
(Ⅰ)求p与q的值;
(Ⅱ)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩优秀与参加数学第二课堂活动有关”.
| 优秀 | 非优秀 | 总计 | |
| 参加数学第二课堂活动 | p | ||
| 未参加数学第二课堂活动 | q | 100 | |
| 总计 | 200 |
(Ⅰ)求p与q的值;
(Ⅱ)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩优秀与参加数学第二课堂活动有关”.
16.曲线y=x3在点x=2处的切线方程是( )
0 247831 247839 247845 247849 247855 247857 247861 247867 247869 247875 247881 247885 247887 247891 247897 247899 247905 247909 247911 247915 247917 247921 247923 247925 247926 247927 247929 247930 247931 247933 247935 247939 247941 247945 247947 247951 247957 247959 247965 247969 247971 247975 247981 247987 247989 247995 247999 248001 248007 248011 248017 248025 266669
| A. | 12x-y-16=0 | B. | 12x+y-32=0 | C. | 4x-y=0 | D. | 4x+y-16=0 |
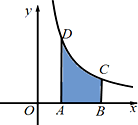 如图,曲边梯形ABCD由直线x=1,x=e,x轴及曲线y=$\frac{3}{x}$围成,则这个曲边梯形的面积是3.(注:e为自然对数的底数)
如图,曲边梯形ABCD由直线x=1,x=e,x轴及曲线y=$\frac{3}{x}$围成,则这个曲边梯形的面积是3.(注:e为自然对数的底数)