题目内容
4.已知幂函数f(x)的图象过点(8,2),则f(-$\frac{1}{8}$)=$-\frac{1}{2}$.分析 设幂函数f(x)=xα(α为常数),把点(8,2)代入解析式求出α的值,再求出f(-$\frac{1}{8}$)的值.
解答 解:设幂函数f(x)=xα,α为常数,
∵f(x)的图象过点(8,2),∴8=2α,解得α=3,
则f(x)=x3,∴f(-$\frac{1}{8}$)=${(-\frac{1}{8})}^{3}$=$-\frac{1}{2}$,
故答案为:$-\frac{1}{2}$.
点评 本题考查幂函数解析式的求法:待定系数法,以及幂函数求值,属于基础题.

练习册系列答案
相关题目
12.某品牌乒乓球按质量标准分为1,2,3,4四个等级,现从某工厂生产的一批乒乓球中随机抽取20个,对其等级进行统计分析,得到的频率分布表如下:
(Ⅰ)在抽取的20个乒乓球中,等级为1的恰有2个,求m,n的值;
(Ⅱ)在(Ⅰ)的条件下,从等级为1和2的乒乓球中任意抽取2个,求抽取的2个乒乓球等级相同的概率.
| 等级 | 1 | 2 | 3 | 4 |
| 频率 | m | n | 0.5 | 0.2 |
(Ⅱ)在(Ⅰ)的条件下,从等级为1和2的乒乓球中任意抽取2个,求抽取的2个乒乓球等级相同的概率.
19.某校高一年级有200人,其中100人参加数学第二课堂活动.在期末考试中,分别对参加数学第二课堂活动的同学与未参加数学第二课堂活动的同学的数学成绩进行调查.按照学生数学成绩优秀与非优秀人数统计后,构成如下不完整的2×2列联表:
已知p是(1+2x)5展开式中的第三项系数,q是(1+2x)5展开式中的第四项的二项式系数.
(Ⅰ)求p与q的值;
(Ⅱ)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩优秀与参加数学第二课堂活动有关”.
| 优秀 | 非优秀 | 总计 | |
| 参加数学第二课堂活动 | p | ||
| 未参加数学第二课堂活动 | q | 100 | |
| 总计 | 200 |
(Ⅰ)求p与q的值;
(Ⅱ)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩优秀与参加数学第二课堂活动有关”.
9.三位男生和一位女生并排照相,若女生不排在两端,则不同的排法共有( )
| A. | 6种 | B. | 12种 | C. | 18种 | D. | 24种 |
16.若圆C的圆心为(2,1),且经过原点O,则圆C的标准方程是( )
| A. | (x-2)2+(y-1)2=$\sqrt{5}$ | B. | (x-2)2+(y-1)2=5 | C. | (x+2)2+(y+1)2=$\sqrt{5}$ | D. | (x+2)2+(y+1)2=5 |
13.执行如图所示的程序框图,若输入x的值为2+log23,则输出y的值为( )
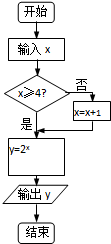

| A. | $\frac{8}{3}$ | B. | 8 | C. | 12 | D. | 24 |
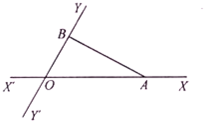 如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.
如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.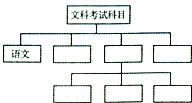 安徽省2015年高考文科考试科目有语文、数学、英语和文综,文综是指政治、历史、地理等三科合在一张卷子上,请你将图补充完整.
安徽省2015年高考文科考试科目有语文、数学、英语和文综,文综是指政治、历史、地理等三科合在一张卷子上,请你将图补充完整.