5.已知四边形ABCD为平行四边形,A(-1,2),B(0,0),C(1,7),则点D的坐标是( )
| A. | (-9,9) | B. | (-9,0) | C. | (0,9) | D. | (0,-9) |
4.要得到函数y=2sin(2x+$\frac{π}{3}$)的图象,只需将函数y=2sinx的图象上所有点( )
| A. | 向左平移$\frac{π}{3}$个单位长度,再把横坐标缩短为原来的2倍(纵坐标不变) | |
| B. | 向左平移$\frac{π}{6}$个单位长度,再把横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变) | |
| C. | 向左平移$\frac{π}{6}$个单位长度,再把横坐标缩短为原来的2倍(纵坐标不变) | |
| D. | 向左平移$\frac{π}{3}$个单位长度,再把横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变) |
1.点M(6,-2$\sqrt{3}$)的极坐标为( )
| A. | (4$\sqrt{3}$,$\frac{π}{6}$) | B. | (4$\sqrt{3}$,$\frac{π}{3}$) | C. | (4$\sqrt{3}$,$\frac{11π}{6}$) | D. | (4$\sqrt{3}$,-$\frac{π}{6}$) |
20.曲线x2+y2=1经过伸缩变换$\left\{\begin{array}{l}{x′=\frac{1}{5}x}\\{y′=\frac{1}{3}y}\end{array}\right.$后,变成的曲线方程是( )
| A. | 25x2+9y2=1 | B. | 9x2+25y2=1 | C. | 25x+9y=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 |
19.复数$\frac{2}{i-1}$的共轭复数是( )
0 247596 247604 247610 247614 247620 247622 247626 247632 247634 247640 247646 247650 247652 247656 247662 247664 247670 247674 247676 247680 247682 247686 247688 247690 247691 247692 247694 247695 247696 247698 247700 247704 247706 247710 247712 247716 247722 247724 247730 247734 247736 247740 247746 247752 247754 247760 247764 247766 247772 247776 247782 247790 266669
| A. | i+1 | B. | i-1 | C. | -1-i | D. | 1-i |
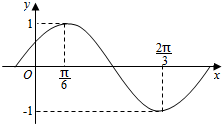 已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.