题目内容

3．（1）在极坐标系中，曲线C1：ρ（$\sqrt{2}$cosθ+sinθ）=1与曲线C2：ρ=α（α＞0）的一个交点在极轴上，求α的值．
（2）在平面直角坐标系中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．已知点A的极坐标为（$\sqrt{2}$，$\frac{π}{4}$），直线的极坐标方程为ρcos（θ-$\frac{π}{4}$）=α，且点A在直线上，求α的值及直线的直角坐标方程．

分析 （1）利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\\{{ρ}^{2}={x}^{2}+{y}^{2}}\end{array}\right.$即可化为直角坐标方程；
（2）同（1）即可得出．

解答 解：（1）曲线C1：ρ（$\sqrt{2}$cosθ+sinθ）=1的普通方程为$\sqrt{2}$x+y=1，曲线C2：ρ=α（α＞0）对应的普通方程为x2+y2=a2．在$\sqrt{2}$x+y=1中，令y=0得x=$\frac{\sqrt{2}}{2}$．
将点$（\frac{\sqrt{2}}{2}，0）$代入x2+y2=a2得$a=\frac{\sqrt{2}}{2}$．
（2）由点A（$\sqrt{2}$，$\frac{π}{4}$），在直线ρcos（θ-$\frac{π}{4}$）=α上可得α=$\sqrt{2}$．
直线方程可化为$\frac{\sqrt{2}}{2}（ρcosθ+ρsinθ）$=$\sqrt{2}$．
∴直线的直角坐标方程为x+y-2=0．

点评 本题考查了极坐标化为直角坐标的方法，属于基础题．

练习册系列答案
相关题目
13．设变量x，y满足$\left\{\begin{array}{l}{x-y≥-1}\\{x+y≥1}\\{3x-y≤3}\end{array}\right.$，则w=4x+y的最大值为（　　）
A．4B．11C．12D．14
14．如图，$|\overrightarrow{AO}|=1$，P是以AB为直径的半圆弧上的动点，以CP为一边作正△CPD，则$|\overrightarrow{OD}|$的最大值是4．
11．如图所示，表示阴影部分的二元一次不等式组是（　　）
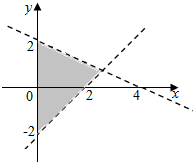
A．$\left\{\begin{array}{l}x-y-2＜0\\ x+2y-4＞0\\ x≥0\end{array}\right.$B．$\left\{\begin{array}{l}x-y-2＜0\\ x+2y-4＜0\\ x≥0\end{array}\right.$
C．$\left\{\begin{array}{l}x-y-2＞0\\ x+2y-4＜0\\ x≥0\end{array}\right.$D．$\left\{\begin{array}{l}x-y-2＞0\\ x+2y-4＞0\\ x≥0\end{array}\right.$
18．如果我们现在手里有6本书，按下列要求各有多少种不同的排法：
（1）6本书有1---6的编号，排成一排，1号和2号必须相邻；
（2）6本书有1---6的编号，排成一排，1号和2号不能相邻；
（3）6本书厚度各不相同，取出3本排成一排，从左到右厚度依次降低．
8．A，B，C，D是空间不共面的四个已知点，它们到平面α的距离都相等，则满足条件的平面α有7个．
15．设数列{an}满足a1=1，an+1=2an+1
（1）求{an}的通项公式；
（2）记bn=log2（an+1），求数列{bn•an}的前n项和为Sn．
12．已知直线l：$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$（t为参数），以坐标原点为极点，x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程是ρ2（1+sin2θ）=2．
（Ⅰ）判断直线l与曲线C的位置关系；
（Ⅱ）已知点P（1，0），当α=$\frac{π}{4}$时，直线l与曲线C交于A，B两点，当α=$\frac{3π}{4}$时，直线l与曲线C交于E，F两点，求|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|+|$\overrightarrow{PE}$|•|$\overrightarrow{PF}$|的值．
13．在数列{an}中，若a1=$\frac{1}{5}$，当n≥2时，有an-1-an-4an-1an=0，则an=4n+1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网