题目内容
7.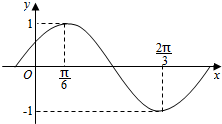 已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.(1)求f(x)的最小正周期及解析式;
(2)求函数g(x)单调递增区间
(3)求函数g(x)在区间x∈[0,$\frac{π}{2}$]上的最大值和最小值.
分析 (1)由图可得A,可求周期T,利用周期公式可求ω,当x=$\frac{π}{6}$时,f(x)=1,可得 sin(2×$\frac{π}{6}$+φ)=1,结合|φ|<$\frac{π}{2}$,可求φ,从而可得f(x)的解析式.
(2)利用三角函数恒等变换可求解析式g(x)=sin(2x-$\frac{π}{6}$),由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z可解得函数g(x)的单调递增区间.
(3)由x∈[0,$\frac{π}{2}$],可求2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],利用正弦函数的图象和性质即可求得函数g(x)在区间x∈[0,$\frac{π}{2}$]上的最大值和最小值.
解答 (本题满分12分)
解:(1)由图可得A=1,(1分)
$\frac{T}{2}=\frac{2π}{3}-\frac{π}{6}=\frac{π}{2}$,所以T=π,
所以$ω=\frac{2π}{π}=2$,(2分)
当x=$\frac{π}{6}$时,f(x)=1,可得 sin(2×$\frac{π}{6}$+φ)=1,
因为|φ|<$\frac{π}{2}$,所以φ=$\frac{π}{6}$,(3分)
所以f(x)的解析式为:f(x)=sin(2x+$\frac{π}{6}$),(4分)
(2)因为g(x)=f(x)-cos2x=sin(2x+$\frac{π}{6}$)-cos2x=sin2xcos$\frac{π}{6}$+cos2xsin$\frac{π}{6}$-cos2x=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x=sin(2x-$\frac{π}{6}$),(6分)
由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z可解得:kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,k∈Z,
所以函数g(x)的单调递增区间是:[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$]k∈Z.(9分)
(3)因为x∈[0,$\frac{π}{2}$],所以2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],(10分)
当2x-$\frac{π}{6}$=$\frac{π}{2}$,即x=$\frac{π}{3}$时,g(x)有最大值,最大值为1;
当2x-$\frac{π}{6}$=-$\frac{π}{6}$,即x=0时,g(x)有最小值,最小值为-$\frac{1}{2}$. (12分).
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数图象与性质,三角函数的恒等变换,三角函数的最值的求法,属于基本知识的考查.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案| A. | 同侧 | B. | (2,3)在直线上 | C. | 异侧 | D. | 以上都不对 |
| A. | $\frac{5π}{12}$rad | B. | $\frac{3π}{7}$rad | C. | $\frac{7π}{12}$rad | D. | $\frac{2π}{9}$rad |