题目内容
2．在极坐标系中，A（3，$\frac{π}{4}$），B（5，-$\frac{π}{12}$）两点间的距离为$\sqrt{19}$．分析 利用余弦定理即可得出．
解答 解：∠AOB=$\frac{π}{4}$-$（-\frac{π}{12}）$=$\frac{π}{3}$．
∴|AB|=$\sqrt{{3}^{2}+{5}^{2}-2×3×5×cos\frac{π}{3}}$=$\sqrt{19}$．
故答案为：$\sqrt{19}$．
点评 本题考查了余弦定理的应用、极坐标的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
12．已知函数f（x）=$\frac{1}{3}$x3-（4m-1）x2+（15m2-2m-7）x+2在R上是增函数，则m的取值范围为（ ）
| A． | m≤2或m≥4 | B． | -4≤m≤-2 | C． | 2≤m≤4 | D． | 以上皆不对 |
10．
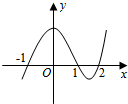设函数f（x）在R上可导，其导函数为f′（x），且函数y=（2-x）f′（x）的图象如图所示，则下列结论中一定成立的是（ ）
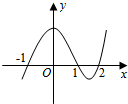设函数f（x）在R上可导，其导函数为f′（x），且函数y=（2-x）f′（x）的图象如图所示，则下列结论中一定成立的是（ ）| A． | 函数f（x）有极大值f（1）和极小值f（-1） | B． | 函数f（x）有极大值f（1）和极小值f（2） | ||
| C． | 函数f（x）有极大值f（2）和极小值f（1） | D． | 函数f（x）有极大值f（-1）和极小值f（2） |
17．在三棱锥P-ABC中，$\overrightarrow{PA}=\vec a$，$\overrightarrow{PB}=\vec b$，$\overrightarrow{PC}=\vec c$，E为棱AB的中点，则$\overrightarrow{CE}$等于（ ）
| A． | $\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | B． | $\vec a+\vec b-\frac{1}{2}\vec c$ | C． | $\frac{1}{2}\vec a+\frac{1}{2}\vec b-\vec c$ | D． | $\frac{1}{2}\vec a+\vec b-\frac{1}{2}\vec c$ |
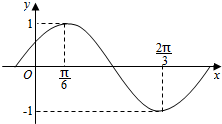已知g（x）=f（x）-cos2x，函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）部分图象如图所示．