12.某商场为了了解顾客的购物信息,随机的在商场收集了100位顾客购物的相关数据,整理如下:
统计结果显示100位顾客中购物款不低于100元的顾客共60位,据统计该商场每日大约有5000名顾客,为了增加商场销售额度,对一次性购物不低于100元的顾客发放纪念品(每人一件).
(Ⅰ)试确定m,n的值,并据上述数据估计该商场每日应准备纪念品的数量;
(Ⅱ)若商场进行让利活动,一次购物款200元及以上的一次返利30元;一次性购物款 小于200元的按购物款的百分比返利,具体见下表:
若用各组购物款的中位数估计该组的购物款,请据上述数据估计该商场日均让利多少元?
| 一次购物款(单位:元) | [0,50) | [50,100) | [100,150) | [150,200) | [200,+∞) |
| 顾客人数 | m | 20 | 30 | n | 10 |
(Ⅰ)试确定m,n的值,并据上述数据估计该商场每日应准备纪念品的数量;
(Ⅱ)若商场进行让利活动,一次购物款200元及以上的一次返利30元;一次性购物款 小于200元的按购物款的百分比返利,具体见下表:
| 一次购物款(单位:元) | [0,50) | [50,100) | [100,150) | [150,200) |
| 返利百分比 | 0 | 6% | 8% | 10% |
11.某校有行政人员、教学人员和教辅人员共200人,其中教学人员与教辅人员人数的比为10:1,行政人员有24人,现采取分层抽样的方法抽取容量为50的样本,那么教学人员应抽取的人数为( )
| A. | 30 | B. | 40 | C. | 20 | D. | 36 |
10.设$a={log_2}π,b={log_{\frac{1}{2}}}π,c=\frac{1}{π^2}$则( )
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
9.已知函数f(x)的反函数为g(x)=1+2x,则f(1)=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
7.在平面直角坐标系xoy中,A、B、C是圆x2+y2=1上相异三点,若存在正实数λ,μ,使得$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$,则λ2+(μ-3)2的取值范围是( )
| A. | [0,+∞) | B. | (2,+∞) | C. | [2,+∞) | D. | (8,+∞) |
6.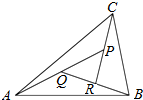 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )| A. | $\frac{1}{2}(\overrightarrow a+\overrightarrow b)$ | B. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | C. | $\frac{2}{7}\overrightarrow a+\frac{4}{7}\overrightarrow b$ | D. | $\frac{4}{7}\overrightarrow a+\frac{2}{7}\overrightarrow b$ |
3.根据给出的数塔猜测123456×9+2等于( )

0 247544 247552 247558 247562 247568 247570 247574 247580 247582 247588 247594 247598 247600 247604 247610 247612 247618 247622 247624 247628 247630 247634 247636 247638 247639 247640 247642 247643 247644 247646 247648 247652 247654 247658 247660 247664 247670 247672 247678 247682 247684 247688 247694 247700 247702 247708 247712 247714 247720 247724 247730 247738 266669

| A. | 111111 | B. | 1111111 | C. | 1111112 | D. | 1111110 |