题目内容
7.在平面直角坐标系xoy中,A、B、C是圆x2+y2=1上相异三点,若存在正实数λ,μ,使得$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$,则λ2+(μ-3)2的取值范围是( )| A. | [0,+∞) | B. | (2,+∞) | C. | [2,+∞) | D. | (8,+∞) |
分析 因为A,B,C互异,所以-1<$\overrightarrow{OB}•\overrightarrow{OC}$<1,由$\overrightarrow{OC}$=$λ\overrightarrow{OA}+μ\overrightarrow{OB}$,得${λ}^{2}=1+{μ}^{2}-2μ\overrightarrow{OB}•\overrightarrow{OC}$,则f(μ)=λ2+(μ-3)2=$1+{μ}^{2}-2μ\overrightarrow{OB}•\overrightarrow{OC}+{(μ-3)}^{2}$=$2{μ}^{2}-6μ-2μ\overrightarrow{OB}•\overrightarrow{OC}+10$,由此能得到λ2+(μ-3)2的取值范围.
解答 解:因为A,B,C,互异,所以-1<$\overrightarrow{OB}•\overrightarrow{OC}$<1,
由$\overrightarrow{OC}$=$λ\overrightarrow{OA}+μ\overrightarrow{OB}$,得${λ}^{2}=1+{μ}^{2}-2μ\overrightarrow{OB}•\overrightarrow{OC}$,
则f(μ)=λ2+(μ-3)2=$1+{μ}^{2}-2μ\overrightarrow{OB}•\overrightarrow{OC}+{(μ-3)}^{2}$=$2{μ}^{2}-6μ-2μ\overrightarrow{OB}•\overrightarrow{OC}+10$>2μ2-8μ+10≥2.
f(μ)=$2{μ}^{2}-6μ-2μ\overrightarrow{OB}•\overrightarrow{OC}+10$<2μ2-4μ+10,无最大值,
∴λ2+(μ-3)2的取值范围是(2,+∞).
故选:B.
点评 本题考查圆的性质和应用以及向量基本定理的应用,综合性较强,有一定的难度.

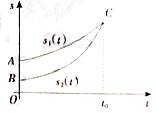 甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )
甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )| A. | v甲>v乙 | B. | v甲<v乙 | C. | v甲=v乙 | D. | 大小关系不确定 |
| A. | 2 | B. | 0 | C. | -1 | D. | -2 |
| 一次购物款(单位:元) | [0,50) | [50,100) | [100,150) | [150,200) | [200,+∞) |
| 顾客人数 | m | 20 | 30 | n | 10 |
(Ⅰ)试确定m,n的值,并据上述数据估计该商场每日应准备纪念品的数量;
(Ⅱ)若商场进行让利活动,一次购物款200元及以上的一次返利30元;一次性购物款 小于200元的按购物款的百分比返利,具体见下表:
| 一次购物款(单位:元) | [0,50) | [50,100) | [100,150) | [150,200) |
| 返利百分比 | 0 | 6% | 8% | 10% |
| A. | f(a)<0,f(b)<0 | B. | f(a)>0,f(b)>0 | C. | f(a)>0,f(b)<0 | D. | f(a)<0,f(b)>0 |

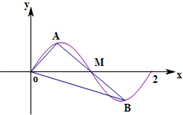 如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )
如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )