设$a={log 2}π.b={log {\frac{1}{2}}}π.c=\frac{1}{π^2}$则( )A．a＞b＞cB．b＞a＞cC．a＞c＞bD．c＞b＞a 题目和参考答案——青夏教育精英家教网—

题目内容

10．设

$a={log_2}π，b={log_{\frac{1}{2}}}π，c=\frac{1}{π^2}$ 则（　　）

A．

a＞b＞c

B．

b＞a＞c

C．

a＞c＞b

D．

c＞b＞a

分析由条件利用对数函数的单调性和特殊点判断出a、b、c的范围，可得它们间的大小关系．

解答解：由于a=log₂π＞1，b= ${log}_{2}\frac{1}{π}$ =-log₂π＜-1，c= $\frac{1}{{π}^{2}}$ ∈（0，1），
∴a＞c＞b，
故选：C．

点评本题主要考查对数函数的单调性和特殊点，属于基础题．

练习册系列答案

智慧课堂密卷100分单元过关检测系列答案

相关题目

20．已知3sin2α=sinα，则cos（α-π）等于（　　）

$\frac{1}{6}$

$-\frac{1}{3}$

$\frac{1}{6}$

$\frac{1}{3}$

$\root{3}{{x}^{2}}$ +3x）ⁿ展开式各项系数和比它的二项式系数和大992．
（1）求展开式中含有x⁴的项；
（2）求展开式中二项式系数最大的项；
（3）求展开式中系数最大的项．

18．“|x|＞1”是“x²-1＞0”的（　　）条件．

	A．	充分而不必要		B．	必要而不充分
	C．	充要		D．	既不充分也不必要

5．已知曲线C的极坐标方程是ρ=2cosθ，直线l的参数方程是

$\left\{\begin{array}{l}x=-\frac{2}{3}t+2\\ y=\frac{2}{3}t-5\end{array}\right.$ （t为参数）．
（1）将曲线C的极坐标方程化为直角坐标方程；
（2）设直线l与y轴的交点是M，N是曲线C上一动点，求MN的最小值．

15．设复数

$z=\frac{{{{（{1+i}）}^2}+3（{1-i}）}}{2+i}$ ，若z²+az+b=1+i，
（1）写出z的实部、虚部；
（2）求实数a，b的值．

2．

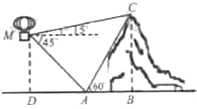如图，在离地面高400m的热气球上，观测到山顶C处的仰角为15°，山脚A处的俯角为45°，已知∠BAC=60°，则山的高度BC为（　　）

$\frac{22π}{3}$ 等于（　　）

$\frac{1}{2}$

$\frac{1}{2}$

$\frac{\sqrt{3}}{2}$

$\frac{\sqrt{3}}{2}$

20．已知函数f（x）=（x²+bx+b）

$\sqrt{1-2x}$ （b∈R）
①当b=-1时，求f（x）的极值．
②若f（x）在区间（0，

$\frac{1}{3}$ ）上单调递增，求b的取值范围．
③试判断f（x）在定义域上的单调性．

试题分类