题目内容
6.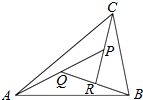 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )| A. | $\frac{1}{2}(\overrightarrow a+\overrightarrow b)$ | B. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | C. | $\frac{2}{7}\overrightarrow a+\frac{4}{7}\overrightarrow b$ | D. | $\frac{4}{7}\overrightarrow a+\frac{2}{7}\overrightarrow b$ |
分析 由向量的三角形法则以及向量中点关系结合向量的基本定理可表示出$\overrightarrow{AP}$.
解答 解:由题意可得$\overrightarrow{AP}$=$\overrightarrow{AC}+\overrightarrow{CP}$=$\overrightarrow{AC}+\frac{1}{2}\overrightarrow{CR}$
=$\overrightarrow{AC}+\frac{1}{2}(\overrightarrow{CB}+\overrightarrow{BR})$=$\overrightarrow{AC}+\frac{1}{2}(\overrightarrow{AB}-\overrightarrow{AC})+\frac{1}{2}\overrightarrow{BR}$
=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}+\frac{1}{4}\overrightarrow{BQ}$=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}+\frac{1}{4}(\overrightarrow{AQ}-\overrightarrow{AB})$
=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}+\frac{1}{4}(\frac{1}{2}\overrightarrow{AP}-\overrightarrow{AB})$
=$\frac{1}{4}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}+\frac{1}{8}\overrightarrow{AP}$,
∴$\frac{7}{8}$$\overrightarrow{AP}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AC}$,
∴$\overrightarrow{AP}$=$\frac{2}{7}\overrightarrow{AB}+\frac{4}{7}\overrightarrow{AC}$=$\frac{2}{7}\overrightarrow{a}+\frac{4}{7}\overrightarrow{b}$,
故选:C.
点评 本题考查平面向量基本定理,表示出$\overrightarrow{AP}$是解决问题的关键,属中档题.

| A. | -5 | B. | 5 | C. | $-\sqrt{5}$ | D. | $\sqrt{5}$ |
| A. | 30 | B. | 40 | C. | 20 | D. | 36 |
| A. | -$\frac{1}{3}<a<\frac{1}{3}$ | B. | a$≤-\frac{1}{3}$ | C. | a$≥\frac{1}{3}$ | D. | 以上都不对 |
| A. | [kπ-$\frac{2π}{3}$,kπ-$\frac{π}{6}$](k∈Z) | B. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | ||
| C. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$](k∈Z) | D. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) |
 如图,将全体正奇数排成一个三角形数阵:按照以上排列的规律,第45行从左向右的第17个数为2013.
如图,将全体正奇数排成一个三角形数阵:按照以上排列的规律,第45行从左向右的第17个数为2013.