13.某校高中三个年级共有学生1800名,各年级男生、女生的人数如表:
已知在高中学生中随机抽取一名同学时,抽到高三年级女生的概率为0.17.
(1)求a的值;
(2)现用分层抽样的方法在全校抽取60名学生,则在高二年级应抽取多少名学生?
(3)已知b≥260,c≥200,求高二年级男生比女生多的概率.
| 高一年级 | 高二年级 | 高三年级 | |
| 男生 | 290 | b | 344 |
| 女生 | 260 | c | a |
(1)求a的值;
(2)现用分层抽样的方法在全校抽取60名学生,则在高二年级应抽取多少名学生?
(3)已知b≥260,c≥200,求高二年级男生比女生多的概率.
12.已知二项式($\sqrt{x}$-$\frac{1}{x}$)n的展开式的第6项是常数项,则n的值是( )
| A. | 5 | B. | 8 | C. | 10 | D. | 15 |
11.二次函数f(x)=ax2+bx+c(a>0)的图象与x轴交点的横坐标为-5和3,则这个二次函数的单调减区间为( )
| A. | (-∞,-1] | B. | [2,+∞) | C. | (-∞,2] | D. | [-1,+∞) |
10.设x,y,z均大于0,则三个数:x+$\frac{1}{y}$,y+$\frac{1}{z}$,z+$\frac{1}{x}$的值( )
| A. | 都大于2 | B. | 至少有一个不大于2 | ||
| C. | 都小于2 | D. | 至少有一个不小于2 |
9.某同学参加高校自主招生3门课程的考试.假设该同学第一门课程取得优秀成绩的概率$\frac{4}{5}$,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{6}{125}$ | x | y | $\frac{24}{125}$ |
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
8.当n为正整数时,定义函数N(n)表示n的最大奇因数.如N(3)=3,N(10)=5,….记S(n)=N(1)+N(2)+N(3)+…+N(2n),则S(4)等于( )
0 247222 247230 247236 247240 247246 247248 247252 247258 247260 247266 247272 247276 247278 247282 247288 247290 247296 247300 247302 247306 247308 247312 247314 247316 247317 247318 247320 247321 247322 247324 247326 247330 247332 247336 247338 247342 247348 247350 247356 247360 247362 247366 247372 247378 247380 247386 247390 247392 247398 247402 247408 247416 266669
| A. | 81 | B. | 82 | C. | 85 | D. | 86 |
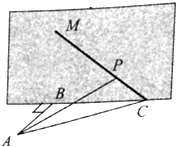 如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若BC=10m,AC=20m,∠BCM=45°,则tanθ的最大值为$\frac{2\sqrt{3}}{3}$.(仰角θ为直线AP与平面ABC所成角)
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若BC=10m,AC=20m,∠BCM=45°,则tanθ的最大值为$\frac{2\sqrt{3}}{3}$.(仰角θ为直线AP与平面ABC所成角)