题目内容
12．已知二项式（$\sqrt{x}$-$\frac{1}{x}$）n的展开式的第6项是常数项，则n的值是（ ）| A． | 5 | B． | 8 | C． | 10 | D． | 15 |
分析 根据二项式展开式的通项公式Tr+1中第6项是常数项，列出方程，求出n的值．
解答 解：∵二项式（$\sqrt{x}$-$\frac{1}{x}$）n的展开式通项公式为
Tr+1=${C}_{n}^{r}$•${（\sqrt{x}）}^{n-r}$•${（-\frac{1}{x}）}^{r}$=（-1）r•${C}_{n}^{r}$•${x}^{\frac{n-3r}{2}}$，
且第6项是常数项，
∴r=5时，$\frac{n-3×5}{2}$=0，
解得n=15；
∴n的值是15．
故选：D．
点评 本题考查了二项式定理的应用问题，也考查了逻辑推理与计算能力，是基础题目．
练习册系列答案
相关题目
2．已知函数f（x）=lnx+$\frac{2a}{x}$，a∈R
（1）若函数f（x）在[1，+∞）上是增函数，求实数a的取值范围；
（2）若函数f（x）在[1，e]上的最小值为2，求实数a的取值范围．
（1）若函数f（x）在[1，+∞）上是增函数，求实数a的取值范围；
（2）若函数f（x）在[1，e]上的最小值为2，求实数a的取值范围．
3．已知a=$\frac{1}{n}$$\underset{\stackrel{n}{∑}}{i=1}$（$\frac{i}{n}$）2（n∈N*），b=${∫}_{0}^{1}$x2dx，则a，b的大小关系为（ ）
| A． | a＜b | B． | a=b | ||
| C． | a＞b | D． | a，b的大小与n的取值有关 |
某校100名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]，则图中a的值为0.005．
17．深圳市某学校为了了解学生使用手机与学习成绩之间的关系，抽查了有手机同学40名，其中成绩为优秀的人数24名，抽查没有手机同学20人，其中成绩为优秀的人数15名，
（1）根据以上数据完成下面的2×2列联表（单位：人）
（2）根据题（1）中表格的数据计算，你有多大的把握，认为学生手机与成绩之间有关系？
（1）根据以上数据完成下面的2×2列联表（单位：人）
| 拥有手机 | 没有手机 | 合计 | |
| 成绩优秀 | |||
| 成绩不优势 | |||
| 合计 |
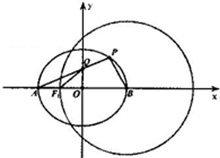如图，点A，B分别是椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，圆B：（x-2）2+y2=9，经过椭圆E的左焦点F．