题目内容
7.函数f(x)=2sinx+x,x∈(0,2π)的单调增区间为$(0,\frac{2π}{3})$和$(\frac{4π}{3},2π)$.分析 先求出函数的导数,结合三角函数的性质解出关于导函数的不等式,从而得到答案.
解答 解:∵f′(x)=2cosx+1,
令f′(x)>0,∴cosx>-$\frac{1}{2}$,
解得:0<x<$\frac{2π}{3}$或$\frac{4π}{3}$<x<2π,
故答案为:$(0,\frac{2π}{3})$和$(\frac{4π}{3},2π)$.
点评 本题考察了函数的单调性问题,考察导数的应用,是一道基础题.

练习册系列答案
相关题目
12.已知二项式($\sqrt{x}$-$\frac{1}{x}$)n的展开式的第6项是常数项,则n的值是( )
| A. | 5 | B. | 8 | C. | 10 | D. | 15 |
15.定义运算a?b为执行如右图所示的程序框图输出的S值,则$({2^-}^{{{log}_2}3})?({log_{\frac{1}{2}}}4)$的值为( )
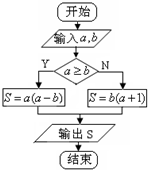

| A. | $\frac{7}{9}$ | B. | $-\frac{8}{3}$ | C. | 4 | D. | -4 |