题目内容
6.已知函数f(x)=lnx+$\frac{3}{8}$x2-2x+2.(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在区间[e2,+∞)(k∈Z)上有零点,求k的最大值(e=2.718…)
分析 (Ⅰ)先求出函数的导数,从而求出函数的单调区间;
(Ⅱ)先求出f(x)在x∈($\frac{2}{3}$,+∞)上没有零点,只需ek<$\frac{2}{3}$即可.通过验证f(e-1),f(e-2)的值,从而求出k的最大值.
解答 解:(Ⅰ)由题知f(x)的定义域为(0,+∞),
因为f′(x)=$\frac{(3x-2)(x-2)}{4x}$,
所以函数f(x)的单调递增区间为(0,$\frac{2}{3}$)和(2,+∞),f(x)的单调递减区间为($\frac{2}{3}$,2);
(II)因为f(x)在x∈($\frac{2}{3}$,+∞)上的最小值为f(2),且
f(2)=$\frac{3}{8}$×22-4+2+ln2=ln2-$\frac{1}{2}$=$\frac{ln4-1}{2}$>0,
故f(x)在x∈($\frac{2}{3}$,+∞)上没有零点.
从而,要想使函数f(x)在[ek,+∞)(k∈z) 上有零点,
并考虑到f(x)在(0,$\frac{2}{3}$)上单调递增,且在($\frac{2}{3}$,2)上单调递减,
故只需ek<$\frac{2}{3}$即可.易验证f(e-1)=$\frac{3}{8}$•e-2-2•e-1+1>0,
f(e-2)=$\frac{3}{8}$•$\frac{1}{{e}^{4}}$-$\frac{2}{{e}^{2}}$+2+lne-2=$\frac{1}{{e}^{2}}$($\frac{3}{8}$$\frac{1}{{e}^{2}}$-2)<0,
当k≤-2且k∈z时均有f(ek)<0,
即函数f(x)在[ek,e-1]?[ek,+∞),(k∈z)上有零点.
所以k的最大值为-2.
点评 本题考察了函数的单调性,考察导数的应用,考察函数的零点问题,本题是一道中档题.

 名校课堂系列答案
名校课堂系列答案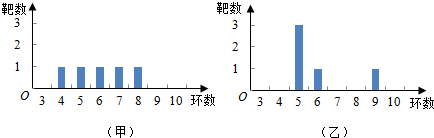
| A. | 甲的成绩的平均数小于乙的成绩的平均数 | |
| B. | 甲的成绩的极差小于乙的成绩的极差 | |
| C. | 甲的成绩的方差小于乙的成绩的方差 | |
| D. | 甲的成绩的中位数等于乙的成绩的中位数 |
| A. | (-∞,-1] | B. | [2,+∞) | C. | (-∞,2] | D. | [-1,+∞) |
| A. | (-∞,4+ln2] | B. | (3,4] | C. | (3,4+ln2] | D. | (2,ln2] |

 三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{{2\sqrt{3}}}{3}$.
三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{{2\sqrt{3}}}{3}$.