8.某同学参加4门学科的学业水平考试,假设该同学第一门学科取得优秀成绩的概率为$\frac{2}{3}$,第二门学科取得优秀成绩的概率为$\frac{4}{5}$,第三、第四门学科取得优秀成绩的概率分别为m,n(m>n),且不同学科是否取得优秀成绩相互独立,记ξ为该同学取得优秀成绩的课程数,其分布列为如下表:
(1)求该生至少有1门课程取得优秀成绩的概率;
(2)求m,n的值;
(3)求数学期望Eξ.
0 247151 247159 247165 247169 247175 247177 247181 247187 247189 247195 247201 247205 247207 247211 247217 247219 247225 247229 247231 247235 247237 247241 247243 247245 247246 247247 247249 247250 247251 247253 247255 247259 247261 247265 247267 247271 247277 247279 247285 247289 247291 247295 247301 247307 247309 247315 247319 247321 247327 247331 247337 247345 266669
| ξ | 0 | 1 | 2 | 3 | 4 |
| p | $\frac{1}{120}$ | x | y | z | $\frac{1}{5}$ |
(2)求m,n的值;
(3)求数学期望Eξ.
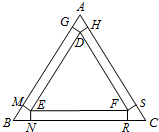 如图:在边长为6米的等边△ABC钢板内,作一个△DEF,使得△DEF的三边到△ABC所对应的三边之间的距离均x(0<x<$\frac{2}{3}$$\sqrt{3}$)米,过点D分别向AB,AC边作垂线,垂足依次为G,H;过点E分别向AB,BC边作垂线,垂足依次为M,N;过点F分别向BC,AC边作垂线,垂足依次为R,S.接着在△ABC的三个内角处,分别沿DG,DH、EM,EN、FR,FS进行切割,割去的三个全等的小四边形分别为AGDH、BMEN、CRFS.然后把矩形GDEM、NEFR、SFDH分别沿DE、EF、FD向上垂直翻折,并对翻折后的钢板进行无缝焊接(注:切割和无缝焊接过程中的损耗和费用忽略不计),从而构成一个无盖的正三棱柱蓄水池.
如图:在边长为6米的等边△ABC钢板内,作一个△DEF,使得△DEF的三边到△ABC所对应的三边之间的距离均x(0<x<$\frac{2}{3}$$\sqrt{3}$)米,过点D分别向AB,AC边作垂线,垂足依次为G,H;过点E分别向AB,BC边作垂线,垂足依次为M,N;过点F分别向BC,AC边作垂线,垂足依次为R,S.接着在△ABC的三个内角处,分别沿DG,DH、EM,EN、FR,FS进行切割,割去的三个全等的小四边形分别为AGDH、BMEN、CRFS.然后把矩形GDEM、NEFR、SFDH分别沿DE、EF、FD向上垂直翻折,并对翻折后的钢板进行无缝焊接(注:切割和无缝焊接过程中的损耗和费用忽略不计),从而构成一个无盖的正三棱柱蓄水池.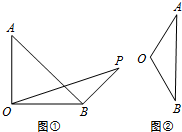 在△AOB中,OA=OB=2,
在△AOB中,OA=OB=2,