题目内容
8.某同学参加4门学科的学业水平考试,假设该同学第一门学科取得优秀成绩的概率为$\frac{2}{3}$,第二门学科取得优秀成绩的概率为$\frac{4}{5}$,第三、第四门学科取得优秀成绩的概率分别为m,n(m>n),且不同学科是否取得优秀成绩相互独立,记ξ为该同学取得优秀成绩的课程数,其分布列为如下表:| ξ | 0 | 1 | 2 | 3 | 4 |
| p | $\frac{1}{120}$ | x | y | z | $\frac{1}{5}$ |
(2)求m,n的值;
(3)求数学期望Eξ.
分析 设事件Ai 表示“该生第i 门课程取得优秀成绩”,其中i=1,2,3,4 由题意知:$P({A_1})=\frac{2}{3}$,$P({A_2})=\frac{4}{5}$,P(A3)=m,P(A4)=n,
(1)利用对立事件的概率,求解即可.
(2)利用P(ξ=0),P(ξ=4)的概率,列出方程,即可求出m、n的值.
(3)利用已知条件求出x,y,z,然后求解期望.
解答 解:设事件Ai 表示“该生第i 门课程取得优秀成绩”,其中i=1,2,3,4 由题意知:$P({A_1})=\frac{2}{3}$,$P({A_2})=\frac{4}{5}$,P(A3)=m,P(A4)=n,
(1)由于事件“该生至少有1门课程取得优秀成绩”与事件“ξ=0”是对立的,所以该生至少有1门课程取得优秀成绩的概率是:$1-P({ξ=0})=1-\frac{1}{120}=\frac{119}{120}$,…3分
(2)由题意可知:$P({ξ=0})=P({\overline{{A_1}{A_2}{A_3}{A_4}}})=\frac{1}{3}×\frac{1}{5}({1-m})({1-n})=\frac{1}{120}$,$P({ξ=4})=P({{A_1}{A_2}{A_3}{A_4}})=\frac{2}{3}×\frac{4}{5}mn=\frac{1}{5}$,
整理得$\left\{\begin{array}{l}m+n=\frac{5}{4}\\ mn=\frac{3}{8}\end{array}\right.$,解之得$\left\{\begin{array}{l}m=\frac{3}{4}\\ n=\frac{1}{2}\end{array}\right.$ 或$\left\{\begin{array}{l}m=\frac{1}{2}\\ n=\frac{3}{4}\end{array}\right.$,
又因为m>n,所以$m=\frac{3}{4},n=\frac{1}{2}$ 即为所求. …8分
(3)又$x=P({ξ=1})=P({{A_1}\overline{{A_2}{A_3}{A_4}}})+P({\overline{A_1}{A_2}\overline{{A_3}{A_4}}})+P({\overline{{A_1}{A_2}}{A_3}\overline{A_4}})+P({\overline{{A_1}{A_2}{A_3}}{A_4}})$
=$\frac{2}{3}×\frac{1}{5}×\frac{1}{4}×\frac{1}{2}+\frac{1}{3}×\frac{4}{5}×\frac{1}{4}×\frac{1}{2}+\frac{1}{3}×\frac{1}{5}×\frac{3}{4}×\frac{1}{2}+\frac{1}{3}×\frac{1}{5}×\frac{1}{4}×\frac{1}{2}=\frac{1}{12}$ …10分 $y=P({ξ=2})=P({{A_1}{A_2}\overline{{A_3}{A_4}}})+P({{A_1}{A_3}\overline{{A_2}{A_4}}})+P({{A_1}{A_4}\overline{{A_2}{A_3}}})+P({{A_2}{A_3}\overline{{A_1}{A_4}}})+P({{A_2}{A_4}\overline{{A_1}{A_3}}})+P({{A_3}{A_4}\overline{{A_1}{A_2}}})$
=$\frac{2}{3}×\frac{4}{5}×\frac{1}{4}×\frac{1}{2}+\frac{2}{3}×\frac{1}{5}×\frac{3}{4}×\frac{1}{2}+\frac{2}{3}×\frac{1}{5}×\frac{1}{4}×\frac{1}{2}+\frac{1}{3}×\frac{4}{5}×\frac{3}{4}×\frac{1}{2}+\frac{1}{3}×\frac{4}{5}×\frac{1}{4}×\frac{1}{2}+\frac{1}{3}×\frac{1}{5}×\frac{3}{4}×\frac{1}{2}=\frac{7}{24}$ …12分
$z=P({ξ=3})=1-P({ξ=0})-P({ξ=1})-P({ξ=2})-P({ξ=4})=1-\frac{1}{120}-\frac{10}{120}-\frac{35}{120}-\frac{24}{120}=\frac{5}{12}$ …14分
则Eξ=0×P(ξ=0)+1×P(ξ=1)+2×P(ξ=2)+3×P(ξ=3)+4×P(ξ=4)
=$0×\frac{1}{120}+1×\frac{10}{120}+2×\frac{35}{120}+3×\frac{50}{120}+4×\frac{24}{120}=\frac{163}{60}$ …16分
点评 本题考查离散型随机变量的分布列期望的求法,考查概率的求法,是中档题.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案方案一:建一保护围墙,需花费4000元,但围墙无法防止大洪水,当大洪水来临时,设备会受损,损失费为30000元.
方案二:不采取措施,希望不发生洪水,此时小洪水来临将损失15000元,大洪水来临将损失30000元.
以下说法正确的是( )
| A. | 方案一的平均损失比方案二的平均损失大 | |
| B. | 方案二的平均损失比方案一的平均损失大 | |
| C. | 方案一的平均损失与方案二的平均损失一样大 | |
| D. | 方案一的平均损失与方案二的平均损失无法计算 |
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
( )
| A. | 40,5 | B. | 50,5 | C. | 5,40 | D. | 5,50 |
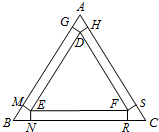 如图:在边长为6米的等边△ABC钢板内,作一个△DEF,使得△DEF的三边到△ABC所对应的三边之间的距离均x(0<x<$\frac{2}{3}$$\sqrt{3}$)米,过点D分别向AB,AC边作垂线,垂足依次为G,H;过点E分别向AB,BC边作垂线,垂足依次为M,N;过点F分别向BC,AC边作垂线,垂足依次为R,S.接着在△ABC的三个内角处,分别沿DG,DH、EM,EN、FR,FS进行切割,割去的三个全等的小四边形分别为AGDH、BMEN、CRFS.然后把矩形GDEM、NEFR、SFDH分别沿DE、EF、FD向上垂直翻折,并对翻折后的钢板进行无缝焊接(注:切割和无缝焊接过程中的损耗和费用忽略不计),从而构成一个无盖的正三棱柱蓄水池.
如图:在边长为6米的等边△ABC钢板内,作一个△DEF,使得△DEF的三边到△ABC所对应的三边之间的距离均x(0<x<$\frac{2}{3}$$\sqrt{3}$)米,过点D分别向AB,AC边作垂线,垂足依次为G,H;过点E分别向AB,BC边作垂线,垂足依次为M,N;过点F分别向BC,AC边作垂线,垂足依次为R,S.接着在△ABC的三个内角处,分别沿DG,DH、EM,EN、FR,FS进行切割,割去的三个全等的小四边形分别为AGDH、BMEN、CRFS.然后把矩形GDEM、NEFR、SFDH分别沿DE、EF、FD向上垂直翻折,并对翻折后的钢板进行无缝焊接(注:切割和无缝焊接过程中的损耗和费用忽略不计),从而构成一个无盖的正三棱柱蓄水池.