题目内容
6.已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合,直线C1的参数方程为$\left\{\begin{array}{l}x=1+tcosα\\ y=tsinα\end{array}$(其中t为参数),曲线C2的极坐标方程为ρsin2θ=4cosθ,(1)求当α=$\frac{π}{6}$时直线C1的普通方程及曲线C2的直角坐标方程;
(2)设F(1,0),直线C1和曲线C2相交于两点A,B,若AF=2FB,求AB的长.
分析 (1)当$α=\frac{π}{6}$ 时,直线C1 的参数方程为$\left\{\begin{array}{l}x=1+\frac{{\sqrt{3}}}{2}t\\ y=\frac{1}{2}t\end{array}\right.$ (其中t 为参数),消去参数t 得,直线C1 的普通方程;线C2 的极坐标方程为$ρ{sin^2}θ=4cos\theta$,即${ρ^2}{sin^2}θ=4ρcos\theta$,把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入即可得出.
(2)直线C1 的普通方程为$y=({x-1})tan\alpha$,且经过点F(1,0),设直线C1 和曲线C2 相交于两点A(x1,y1),B(x2,y2),联立方程化为tanαy2-4y-4tanα=0,解之得y1,2,利用AF=2FB,可得tan2α=8,利用弦长公式$AB=\sqrt{{{({{x_1}-{x_2}})}^2}+{{({{y_1}-{y_2}})}^2}}=\sqrt{1+\frac{1}{{{{tan}^2}α}}}|{{y_1}-{y_2}}|$即可得出.
解答 解:(1)当$α=\frac{π}{6}$ 时,直线C1 的参数方程为$\left\{\begin{array}{l}x=1+\frac{{\sqrt{3}}}{2}t\\ y=\frac{1}{2}t\end{array}\right.$ (其中t 为参数),
消去参数t 得,直线C1 的普通方程为$x-\sqrt{3}y-1=0$;
曲线C2 的极坐标方程为$ρ{sin^2}θ=4cos\theta$,即${ρ^2}{sin^2}θ=4ρcos\theta$,
即y2=4x 为曲线C2 的直角坐标方程.
(2)直线C1 的普通方程为$y=({x-1})tan\alpha$,且经过点F(1,0),
设直线C1和曲线C2相交于两点A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}y=({x-1})tanα\\{y^2}=4x\end{array}\right.$,消去变量x 可整理得,tanαy2-4y-4tanα=0,
解之得${y_{1,2}}=\frac{{4±4\sqrt{1+{{tan}^2}α}}}{2tanα}=\frac{{2±2\sqrt{1+{{tan}^2}α}}}{tanα}$,
∵AF=2FB,
∴$|{\frac{{2+2\sqrt{1+{{tan}^2}α}}}{tanα}}|=2|{\frac{{2-2\sqrt{1+{{tan}^2}α}}}{tanα}}|$,即tan2α=8,
∴$AB=\sqrt{{{({{x_1}-{x_2}})}^2}+{{({{y_1}-{y_2}})}^2}}=\sqrt{1+\frac{1}{{{{tan}^2}α}}}|{{y_1}-{y_2}}|$=$\sqrt{1+\frac{1}{{{{tan}^2}α}}}\frac{{4\sqrt{1+{{tan}^2}α}}}{{|{tanα}|}}=\frac{{4({1+{{tan}^2}α})}}{{{{tan}^2}α}}=\frac{9}{2}$.
点评 本题考查了曲线的参数方程化为直角坐标方程、极坐标方程化为直角坐标方程、直线与抛物线相交弦长问题,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
 已知△ABC中,角A,B,C所对的边分别为a,b,c,若sin2 A+sin2 B=sin2C+sin AsinB,ccosB=b(1-cosC).
已知△ABC中,角A,B,C所对的边分别为a,b,c,若sin2 A+sin2 B=sin2C+sin AsinB,ccosB=b(1-cosC).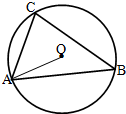 如图所示,在△ABC中,AB=4,AC=2,若O为△ABC的外心.
如图所示,在△ABC中,AB=4,AC=2,若O为△ABC的外心. 如图,用X、Y、Z这3类不同的元件连接成系统N,每个元件是否正常工作不受其它元件的影响,已知元件X、Y、Z正常工作的概率依次为0.8、0.7、0.9,则系统N正常工作的概率是0.776.
如图,用X、Y、Z这3类不同的元件连接成系统N,每个元件是否正常工作不受其它元件的影响,已知元件X、Y、Z正常工作的概率依次为0.8、0.7、0.9,则系统N正常工作的概率是0.776.