题目内容
11.已知$\overrightarrow{m}$=(sinωx,-1),$\overrightarrow{n}$=(1,-$\sqrt{3}$cosωx)(其中x∈R,ω>0),f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$,且函数f(x)图象的某个最高点到其相邻的最低点之间的距离为5,(1)求函数f(x)的单调递增区间;
(2)若f($\frac{3θ}{π}$)=$\frac{6}{5}$(其中θ∈(-$\frac{5π}{6}$,$\frac{π}{6}$),则求f($\frac{6θ}{π}$+1)的取值.
分析 (1)利用$f(x)=\overrightarrow m•\overrightarrow n$,结合两角和与差的三角函数化简函数的解析式,求解函数的周期,得到函数的解析式,利用子线盒的单调性求解单调增区间.
(2)利用条件求出$sin({θ+\frac{π}{3}})=\frac{3}{5}$,得到$cos(θ+\frac{π}{3})$,通过二倍角公式求解即可.
解答 (本小题满分14分)
解:(1)∵$\overrightarrow m=({sinωx,-1})$,$\overrightarrow n=({1,-\sqrt{3}cosωx})$(其中x∈R,ω>0),$f(x)=\overrightarrow m•\overrightarrow n$,
∴$f(x)=sinωx+\sqrt{3}cosωx=2sin({ωx+\frac{π}{3}})$,…(2分)
又∵函数f(x)图象的某个最高点到其相邻的最低点之间的距离为5,
∴$\sqrt{{4^2}+{{({\frac{T}{2}})}^2}}=5$,解之得:T=6,…(4分)
又$T=\frac{2π}{ω}$,则$ω=\frac{2π}{T}=\frac{π}{3}$,即$f(x)=2sin({\frac{π}{3}x+\frac{π}{3}})$,…(6分)
则$2kπ-\frac{π}{2}≤\frac{π}{3}x+\frac{π}{3}≤2kπ+\frac{π}{2}$,
即$6k-\frac{5}{2}≤x≤6k+\frac{1}{2}({k∈Z})$,
即所求函数f(x)的单调递增区间为$[{6k-\frac{5}{2},6k+\frac{1}{2}}]({k∈Z})$…(8分)
(2)由(1)可知$f(x)=2sin({\frac{π}{3}x+\frac{π}{3}})$,
则$f({\frac{3θ}{π}})=2sin({\frac{π}{3}•\frac{3θ}{π}+\frac{π}{3}})=2sin({θ+\frac{π}{3}})=\frac{6}{5}$,
即$sin({θ+\frac{π}{3}})=\frac{3}{5}$…(10分)
∵$θ∈({-\frac{5π}{6},\frac{π}{6}})$,∴$θ+\frac{π}{3}∈({-\frac{π}{2},\frac{π}{2}})$,则$cos({θ+\frac{π}{3}})>0$
即$cos({θ+\frac{π}{3}})=\sqrt{1-{{sin}^2}({θ+\frac{π}{3}})}=\frac{4}{5}$,…(12分)
也即$f({\frac{6θ}{π}+1})=2sin[{\frac{π}{3}({\frac{6θ}{π}+1})+\frac{π}{3}}]=2sin[{2({θ+\frac{π}{3}})}]$=$4sin({θ+\frac{π}{3}})cos({θ+\frac{π}{3}})=\frac{48}{25}$…(14分)
点评 本题考查三角函数的化简求值,斜率的数量积的应用,两角和与差的三角函数,考查计算能力.

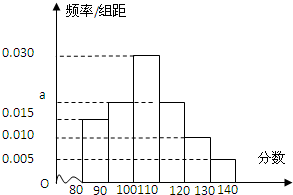 某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )
某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )| A. | 36 | B. | 27 | C. | 22 | D. | 11 |
| A. | $\frac{23}{3}$ | B. | $\frac{22}{3}$ | C. | $\frac{47}{6}$ | D. | 7 |
(Ⅰ)设甲停车付费a元.依据题意,填写下表:
| 甲停车时长 (小时) | (0,1] | (1,2] | (2,3] | (3,4] |
| 甲停车费a (元) |
(Ⅲ)若甲停车1小时以上且不超过2小时的概率为$\frac{1}{3}$,停车付费多于14元的概率为$\frac{5}{12}$,求甲停车付费恰为6元的概率.