6.设函数y=f(x)定义在实数集R上,则函数y=f(1-x)与y=f(x-1)的图象关于( )
| A. | 直线y=0对称 | B. | 直线x=0对称 | C. | 直线y=1对称 | D. | 直线x=1对称 |
5.设△ABC的三边a、b、c成等差数列,则tan$\frac{A}{2}$tan$\frac{C}{2}$的值( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
4.已知cosα=$\frac{4}{5}$,α∈(-$\frac{π}{2}$,0),则tan($\frac{π}{4}$+$\frac{α}{2}$)的值是( )
| A. | 2 | B. | $\frac{2}{5}$ | C. | -2 | D. | -$\frac{1}{2}$ |
3.已知奇函数f(x)的定义域为(2a,a+1),求f(a+$\frac{1}{3}$)的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
2.求函数y=cos$\frac{11π}{12}$的值( )
0 246920 246928 246934 246938 246944 246946 246950 246956 246958 246964 246970 246974 246976 246980 246986 246988 246994 246998 247000 247004 247006 247010 247012 247014 247015 247016 247018 247019 247020 247022 247024 247028 247030 247034 247036 247040 247046 247048 247054 247058 247060 247064 247070 247076 247078 247084 247088 247090 247096 247100 247106 247114 266669
| A. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | C. | $\frac{-\sqrt{6}-\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
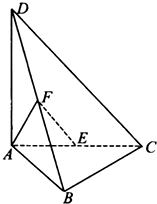 如图,四面体ABCD中,AD⊥平面ABC,AB⊥BC,E,F分别为AC,BD的中点,AB=AD=2,∠BAC=60°.
如图,四面体ABCD中,AD⊥平面ABC,AB⊥BC,E,F分别为AC,BD的中点,AB=AD=2,∠BAC=60°.