题目内容
4.已知cosα=$\frac{4}{5}$,α∈(-$\frac{π}{2}$,0),则tan($\frac{π}{4}$+$\frac{α}{2}$)的值是( )| A. | 2 | B. | $\frac{2}{5}$ | C. | -2 | D. | -$\frac{1}{2}$ |
分析 先cosα=$\frac{4}{5}$,α∈(-$\frac{π}{2}$,0),求得tan$\frac{α}{2}$,再利用和角的正切公式,即可得到结论.
解答 解:∵cosα=$\frac{4}{5}$,α∈(-$\frac{π}{2}$,0),tan$\frac{α}{2}$=$\frac{sin\frac{α}{2}}{cos\frac{α}{2}}$=$\frac{sinα}{2co{s}^{2}\frac{α}{2}}$=$\frac{sinα}{1+cosα}$=$\frac{-\frac{3}{5}}{1+\frac{4}{5}}$=-$\frac{1}{3}$,
tan($\frac{π}{4}$+$\frac{α}{2}$)=$\frac{tan\frac{π}{4}+tan\frac{α}{2}}{1-tan\frac{π}{4}tan\frac{α}{2}}$=$\frac{1-\frac{1}{3}}{1+\frac{1}{3}}$=$\frac{1}{2}$.
故选:D.
点评 本题考查两角和与差的三角函数,半角的三角函数,考查二倍角公式,正确运用公式是关键.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | 命题“若x=y,则sinx=siny”的否命题为真命题 | |
| B. | “直线x-ay=0与直线x+ay=0互相垂直”的充分条件是“a=1” | |
| C. | 命题“?x∈R,x2+x+1<0”的否定是“?x∈R,x2+x+1>0” | |
| D. | 命题:若x2=1,则x=1或x=-1的逆否命题为:若x≠1或x≠-1,则x2≠1 |
12.随着人们低碳出行意识的提高,低碳节能小排量(小于或等于1.3L)汽车阅历越受私家购买者青睐,工信部为比较A,B两种小排量汽车的100km综合工况油耗,各随机选100辆汽车进行综合工况油耗检测,表1和表2分别是汽车A额B的综合工况检测的结果.
表1:A种汽车综合工况油耗的频数分布表
表2:B种汽车综合工况油耗的频数分布表
(1)完成下面频数分布直观图;
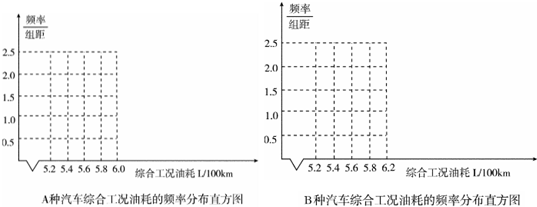
(2)据此样本分析,估计1000辆A种汽车都行驶100km的综合工况油耗总量约为多少(单位:L)(同一组中的数据用该区间的中点值做代表).
(3)完成下面2×2列联表,并回答是否有95%的把握认为“A中汽车与B中汽车的100km综合工况油耗由差异”:
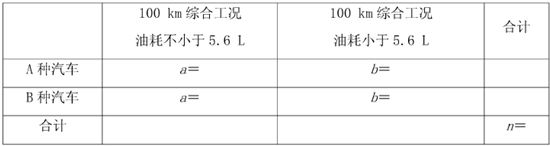
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(b+d)}$,其中,n=a+b+c+d.
表1:A种汽车综合工况油耗的频数分布表
| 100km综合工况油耗(L) | [5.2,5.4) | [5.4,5.6) | [5.6,5.8) | [5.8,6.0] |
| 频数 | 10 | 20 | 40 | 30 |
| 100km综合工况油耗(L) | [5.2,5.4) | [5.2,5.4) | [5.6,5.8) | [5.8,6.0) | [6.0,6.2] |
| 频数 | 15 | 30 | 20 | 25 | 10 |

(2)据此样本分析,估计1000辆A种汽车都行驶100km的综合工况油耗总量约为多少(单位:L)(同一组中的数据用该区间的中点值做代表).
(3)完成下面2×2列联表,并回答是否有95%的把握认为“A中汽车与B中汽车的100km综合工况油耗由差异”:

附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(b+d)}$,其中,n=a+b+c+d.
| P(K2≥k0) | 0.100 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
16.各项均为正数的等差数列{an}中,a4a9=36,则前12项和S12的最小值为( )
| A. | 78 | B. | 48 | C. | 60 | D. | 72 |
13.已知数列 {an}{bn}满足 a1=b1=1,an+1-an=$\frac{{b}_{n+1}}{{b}_{n}}$=2,n∈N*,则数列 {b${\;}_{{a}_{n}}$}的前10项和为( )
| A. | $\frac{1}{3}$(410-1) | B. | $\frac{4}{3}$(410-1) | C. | $\frac{1}{3}$(49-1) | D. | $\frac{4}{3}$(49-1) |
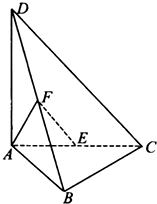 如图,四面体ABCD中,AD⊥平面ABC,AB⊥BC,E,F分别为AC,BD的中点,AB=AD=2,∠BAC=60°.
如图,四面体ABCD中,AD⊥平面ABC,AB⊥BC,E,F分别为AC,BD的中点,AB=AD=2,∠BAC=60°.