题目内容
11.已知f(x)=sinxsin(x+$\frac{π}{6}$),$x∈[-\frac{π}{3},\frac{π}{3}]$,则f(x)的最小值为$\frac{\sqrt{3}-2}{4}$.分析 利用两角和公式对函数解析式化简整理,进而根据三角函数图象与性质求得最小值.
解答 解:f(x)=sinxsin(x+$\frac{π}{6}$)=sinx($\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx)=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$sinxcosx=$\frac{1}{4}$sin2x-$\frac{\sqrt{3}}{4}$cos2x+$\frac{\sqrt{3}}{4}$=$\frac{1}{2}$sin(2x-$\frac{π}{3}$)+$\frac{\sqrt{3}}{4}$,
∴当sin(2x-$\frac{π}{3}$)=-1时,f(x)有最小值$\frac{\sqrt{3}-2}{4}$,
故答案为:$\frac{\sqrt{3}-2}{4}$.
点评 本题主要考查了两角和与差的正弦函数,三角函数图象与性质.考查了学生对三角函数基础公式的灵活运用.

练习册系列答案
相关题目
1.已知 m、n 是两条不重合的直线,α、β、γ是三个互不重合的平面,则下列命题中 正确的是( )
| A. | 若 m∥α,n∥α,则 m∥n | B. | 若α⊥γ,β⊥γ,则 α∥β | ||
| C. | 若m⊥α,n⊥α,则 m∥n | D. | 若 m∥α,m∥β,则 α∥β |
2.设集合U={1,2,3,4,5},A={1,3},B={2,3,4},则(CUA)∩(CUB)=( )
| A. | {1} | B. | {5} | C. | {2,4} | D. | {1,2,4,5} |
6.设函数y=f(x)定义在实数集R上,则函数y=f(1-x)与y=f(x-1)的图象关于( )
| A. | 直线y=0对称 | B. | 直线x=0对称 | C. | 直线y=1对称 | D. | 直线x=1对称 |
16.各项均为正数的等差数列{an}中,a4a9=36,则前12项和S12的最小值为( )
| A. | 78 | B. | 48 | C. | 60 | D. | 72 |
3.函数f(x)=log2(x+2)-$\frac{3}{x}$(x>0)的零点所在的大致区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,e) | D. | (3,4) |
1.一只小狗在如图所示的方砖上走来走去,求最终停在阴影方砖上的概率为( )
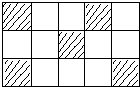

| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |