12.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),F1,F2分别为其左、右焦点,若其右支上存在点P满足$\frac{{|{\overrightarrow{P{F_1}}}|}}{{|{\overrightarrow{P{F_2}}}|}}$=e(e为双曲线C的离心率),则e的最大值为( )
| A. | 4$\sqrt{2}$ | B. | 3+$\sqrt{5}$ | C. | 2$\sqrt{2}$+1 | D. | 3+2$\sqrt{2}$ |
11.在正方体ABCD-A′B′C′D′中,过对角线BD'的一个平面交AA′于点E,交CC′于点F.则下列结论正确的是( )
①四边形BFD′E一定是平行四边形
②四边形BFD′E有可能是正方形
③四边形BFD′E在底面ABCD的投影一定是正方形
④四边形BFD′E有可能垂于于平面BB′D.
①四边形BFD′E一定是平行四边形
②四边形BFD′E有可能是正方形
③四边形BFD′E在底面ABCD的投影一定是正方形
④四边形BFD′E有可能垂于于平面BB′D.
| A. | ①②③④ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
6.点M(x,y)在直线x+y-10=0上,且x,y满足-5≤x-y≤5,则$\sqrt{{x}^{2}+{y}^{2}}$的取值范围是( )
| A. | [0,$\frac{5\sqrt{10}}{2}$] | B. | [0,5$\sqrt{2}$] | C. | [5$\sqrt{2}$,$\frac{5\sqrt{10}}{2}$] | D. | [5,$\frac{5\sqrt{10}}{2}$] |
5.已知复数z满足方程z+i=zi(i为虚数单位),则复数$\overline{z}$对应点在第几象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4. 如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )
如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )
0 246818 246826 246832 246836 246842 246844 246848 246854 246856 246862 246868 246872 246874 246878 246884 246886 246892 246896 246898 246902 246904 246908 246910 246912 246913 246914 246916 246917 246918 246920 246922 246926 246928 246932 246934 246938 246944 246946 246952 246956 246958 246962 246968 246974 246976 246982 246986 246988 246994 246998 247004 247012 266669
 如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )
如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 3 |
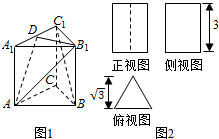 已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.
已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.