题目内容
12.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),F1,F2分别为其左、右焦点,若其右支上存在点P满足$\frac{{|{\overrightarrow{P{F_1}}}|}}{{|{\overrightarrow{P{F_2}}}|}}$=e(e为双曲线C的离心率),则e的最大值为( )| A. | 4$\sqrt{2}$ | B. | 3+$\sqrt{5}$ | C. | 2$\sqrt{2}$+1 | D. | 3+2$\sqrt{2}$ |
分析 设P点的横坐标为x,根据|PF1|=e|PF2|,P在双曲线右支(x≥a),利用双曲线的第二定义,可得x关于e的表达式,进而根据x的范围确定e的范围.
解答 解:设P点的横坐标为x,准线方程为x=±$\frac{{a}^{2}}{c}$,
∵|PF1|=e|PF2|,P在双曲线右支(x≥a),
根据双曲线的第二定义,可得e2(x-$\frac{{a}^{2}}{c}$)=e(x+$\frac{{a}^{2}}{c}$),
∴(e-1)x=$\frac{{a}^{2}}{c}$+a
∵x≥a,
∴$\frac{{a}^{2}}{c}$+a≥(e-1)a,∴e2-2e-1≤0
∵e>1,∴1<e≤2$\sqrt{2}$+1,
则双曲线的离心率的最大值为2$\sqrt{2}$+1.
故选:C.
点评 本题主要考查了双曲线的简单性质,考查了双曲线的第二定义的灵活运用,属于基础题.

练习册系列答案
相关题目
17.某班的一次数学考试后,按学号统计前20名同学的考试成绩如茎叶图所示,则该样本数据的中位数为( )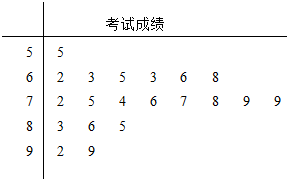

| A. | 74.5 | B. | 75 | C. | 75.5 | D. | 76 |
2. 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )
 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )| A. | 100 | B. | 120 | C. | 130 | D. | 390 |
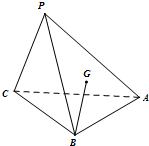 点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.
点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心. 如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.
如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.