题目内容
9.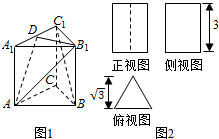 已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.
已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.(1)求证:BC1∥平面AB1D
(2)求二面角B1-AD-B的余弦值.
分析 由三视图可知:该几何体是一个正三棱柱,底面是高为$\sqrt{3}$的正三角形,三棱柱的高为h=3.
(1)利用三角形的中位线定理和线面平行的判定定理即可证明;
(2)通过建立空间直角坐标系,利用两平面的法向量的夹角即可得到两平面所成的锐二面角的余弦值.
解答 (1)证明:由三视图可知:该几何体是一个正三棱柱,底面是高为$\sqrt{3}$的正三角形,三棱柱的高为h=3.
连接A1B交AB1于点E,连接DE,由矩形ABB1A1,可得A1E=EB.
又∵D是这个几何体的棱A1 C1的中点,∴ED是三角形A1BC1的中位线,∴ED∥BC1
∵BC1?平面AB1D,OD?平面AB1D,∴BC1∥平面AB1D.
(2)解:在平面ABC内作AN⊥AB,分别以AB,AN,AA1为x轴,y轴,z轴建立空间直角坐标系.
则A(0,0,0),B1(2,0,3),D($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,3),B(2,0,0).
∴$\overrightarrow{A{B}_{1}}$=(2,0,3),$\overrightarrow{AD}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,3),.
设平面AB1D的法向量为$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{2a+3c=0}\\{\frac{1}{2}a+\frac{\sqrt{3}}{2}b+3c=0}\end{array}\right.$,令a=1,得$\overrightarrow{m}$=(1,$\sqrt{3}$,-$\frac{2}{3}$).
同理平面ABD的法向量$\overrightarrow{n}$=(0,-6,$\sqrt{3}$).
∴cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\sqrt{130}}{13}$.
点评 由三视图可得出该几何体是一个正三棱柱,熟练掌握三角形的中位线定理和线面平行的判定定理、通过建立空间直角坐标系并利用两平面的法向量的夹角求得两平面所成的锐二面角的余弦值是解题的关键.

| A. | $(1,\sqrt{2}]$ | B. | $[\sqrt{2},+∞)$ | C. | $(1,\sqrt{3}]$ | D. | $[\sqrt{3},+∞)$ |

| A. | 11? | B. | 12? | C. | 13? | D. | 14? |
 如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )
如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 3 |
| A. | 2 | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{3}$+1 |
| A. | 在圆外 | B. | 在圆上 | C. | 在圆内 | D. | 不能确定 |