题目内容
4. 如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )
如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 3 |
分析 设$\overrightarrow{BP}$=n$\overrightarrow{BN}$,利用向量的线性运算,结合$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,可求实数m的值.
解答 解:由题意,设$\overrightarrow{BP}$=n$\overrightarrow{BN}$,
则 $\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{BP}$=$\overrightarrow{AB}$+n$\overrightarrow{BN}$=$\overrightarrow{AB}$+n($\overrightarrow{AN}$-$\overrightarrow{AB}$)=$\overrightarrow{AB}$+n($\frac{1}{4}$$\overrightarrow{NC}$-$\overrightarrow{AB}$)=$\overrightarrow{AB}$+n($\frac{1}{5}$$\overrightarrow{AC}$-$\overrightarrow{AB}$)=(1-n)$\overrightarrow{AB}$+$\frac{n}{5}$$\overrightarrow{AC}$,
又∵$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,
∴m=1-n,且$\frac{n}{5}$=$\frac{1}{6}$
解得;n=$\frac{5}{6}$,m=$\frac{1}{6}$,
故选:A
点评 本题考查向量的线性运算,考查学生分析解决问题的能力,属于中档题.

| A. | {2,4,5} | B. | {1,3,5} | C. | {2,4} | D. | {1,2,3,4,5} |
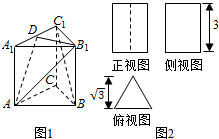 已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.
已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.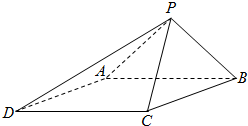 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.