题目内容
11.在正方体ABCD-A′B′C′D′中,过对角线BD'的一个平面交AA′于点E,交CC′于点F.则下列结论正确的是( )①四边形BFD′E一定是平行四边形
②四边形BFD′E有可能是正方形
③四边形BFD′E在底面ABCD的投影一定是正方形
④四边形BFD′E有可能垂于于平面BB′D.
| A. | ①②③④ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
分析 ①根据一个面与两个平行的面的交线一定平行的性质证明出四边形BFD′E一定是平行四边形.
②先看F与C′重合,E与A点重合时不可能是正方形,在看不重合时BF和BE不可能垂直,进而推断结论不正确.
③四边形BFD′E在底面ABCD的投影是正方体的底面,进而可知,射影一定是正方形.
④找到E,F分别为中点时,利用证明EF⊥面BDD′B′,进而证明出两个面垂直.
解答 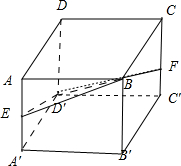 解:
解:
①∵四边形BFD′E与面BCC′B′的交线为BF,与面ADD′A′的交线为D′E,且面BCC′B′∥面ADD′A′的交线为D′E,
∴BF∥D′E,
同理可证明出BE∥D′F,
∴四边形BFD′E一定是平行四边形,
故结论①正确.
②当F与C′重合,E与A点重合时,BF显然与EB不相等,不能是正方形,
当这不重合时,BF和BE不可能垂直,
综合可知,四边形BFD′E不可能是正方形
结论②错误.
③∵四边形BFD′E在底面ABCD的投影是四边形A′B′C′D′,
故一定是正方形,③结论正确.
④当E,F分别是AA′,CC′的中点时,
EF∥AC,AC⊥BD,
∴EF⊥BD,
BB′⊥面ABCD,AC?面ABCD,
∴BB′⊥AC,
∴BB′⊥EF,
∵BB′?面BDD′B′,BD?面BDD′B′,BD∩BB′=B,
∴EF⊥面BDD′B′,
∵EF?四边形BFD′E,平面BB′D?面BDD′B′,
∴面形BFD′E⊥面BDD′B′.
故结论④正确.
故选:B.
点评 本题主要考查了线面垂直的判定定理的应用.有些地方,需要找一些特殊点来解决,比如第④结论找到中点的情况.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.点M(x,y)在直线x+y-10=0上,且x,y满足-5≤x-y≤5,则$\sqrt{{x}^{2}+{y}^{2}}$的取值范围是( )
| A. | [0,$\frac{5\sqrt{10}}{2}$] | B. | [0,5$\sqrt{2}$] | C. | [5$\sqrt{2}$,$\frac{5\sqrt{10}}{2}$] | D. | [5,$\frac{5\sqrt{10}}{2}$] |
16.已知集合M={1,2,3,4},N={2,4,5},则{x|x∈M∪N,x∉M∩N}=( )
| A. | {2,4,5} | B. | {1,3,5} | C. | {2,4} | D. | {1,2,3,4,5} |
20.已知函数f(x)=x3-mx,x∈R,若方程f(x)=2在x∈[-4,4]恰有3个不同的实数解,则实数m的取值范围是( )
| A. | $({-\frac{31}{2},3}]$ | B. | $({3,\frac{31}{2}}]$ | C. | $({-∞,-3})∪({\frac{31}{2},+∞})$ | D. | $({-∞,3})∪({\frac{31}{2},+∞})$ |
1.已知$\frac{m}{1+i}$=1-ni,其中m,n是实数,i是虚数单位,则m+n=( )
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
 如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2CD=2,侧面APD为等腰直角
如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2CD=2,侧面APD为等腰直角