17.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若$\overrightarrow{PF}$=3$\overrightarrow{QF}$,则|QF|=( )
| A. | $\frac{5}{2}$ | B. | $\frac{8}{3}$ | C. | 3 | D. | 6 |
13.某校对数学、物理两科进行学业水平考前辅导,辅导后进行测试,按成绩(满分100分)划分为合格(成绩大于或等于70分)和不合格(成绩小于70分).现随机抽取两科各100名学生的成绩统计如下:
(1)试分别估计该校学生数学、物理合格的概率;
(2)数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作
时间;物理合格一人可赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人所赢得的机器人操作时间(单位:小时)总和,求随机变量X 的分布列和数学期望;
(ii)随机抽取5名学生,求这5名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于14小时的概率.
| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
(2)数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作
时间;物理合格一人可赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人所赢得的机器人操作时间(单位:小时)总和,求随机变量X 的分布列和数学期望;
(ii)随机抽取5名学生,求这5名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于14小时的概率.
12.已知0<x1<x2<x3,a=$\frac{{{{log}_2}(2{x_1}+2)}}{x_1},b=\frac{{{{log}_2}(2{x_2}+2)}}{x_2},c=\frac{{{{log}_2}(2{x_3}+2)}}{x_3}$,则a、b、c的大小关系为( )
| A. | c<a<b | B. | b<a<c | C. | a<b<c | D. | c<b<a |
11.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如表:
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜和韭菜的种植面积(单位:亩)分别为30;20.
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
10.将1~9这9个数平均分成3组,则每组的3个数都成等差数列的分组方法的种数是( )
0 246770 246778 246784 246788 246794 246796 246800 246806 246808 246814 246820 246824 246826 246830 246836 246838 246844 246848 246850 246854 246856 246860 246862 246864 246865 246866 246868 246869 246870 246872 246874 246878 246880 246884 246886 246890 246896 246898 246904 246908 246910 246914 246920 246926 246928 246934 246938 246940 246946 246950 246956 246964 266669
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
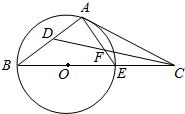 如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A是切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点F.
如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A是切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点F.