题目内容
9.在直角三角形ABC中,∠C=$\frac{π}{2}$,AB=2,AC=1,若$\overrightarrow{AD}$=$\frac{3}{2}$$\overrightarrow{AB}$,则$\overrightarrow{CD}$•$\overrightarrow{CB}$=$\frac{9}{2}$.分析 根据结合图形得出$\overrightarrow{CD}$=$\overrightarrow{CA}$$+\overrightarrow{AD}$=$\overrightarrow{CA}$$+\frac{3}{2}$$\overrightarrow{AB}$,$\overrightarrow{CA}$$•\overrightarrow{CB}$=0,$\overrightarrow{AB}$$•\overrightarrow{CB}$=2×$\sqrt{3}$×COS30°,转化得出$\overrightarrow{CD}$•$\overrightarrow{CB}$=($\overrightarrow{CA}$$+\frac{3}{2}$$\overrightarrow{AB}$)•$\overrightarrow{CB}$=$\overrightarrow{CA}$$•\overrightarrow{CB}$+$\frac{3}{2}$$\overrightarrow{AB}$$•\overrightarrow{CB}$求解即可.
解答 解:∵直角三角形ABC中,∠C=$\frac{π}{2}$,AB=2,AC=1,
∴根据勾股定理得出BC=$\sqrt{3}$,sin∠ABC═$\frac{AC}{AB}$=$\frac{1}{2}$,即∠ABC=30°
∵若$\overrightarrow{AD}$=$\frac{3}{2}$$\overrightarrow{AB}$,
∴$\overrightarrow{CD}$=$\overrightarrow{CA}$$+\overrightarrow{AD}$=$\overrightarrow{CA}$$+\frac{3}{2}$$\overrightarrow{AB}$,$\overrightarrow{CA}$$•\overrightarrow{CB}$=0,$\overrightarrow{AB}$$•\overrightarrow{CB}$=2×$\sqrt{3}$×COS30°=3
∴$\overrightarrow{CD}$•$\overrightarrow{CB}$=($\overrightarrow{CA}$$+\frac{3}{2}$$\overrightarrow{AB}$)•$\overrightarrow{CB}$=$\overrightarrow{CA}$$•\overrightarrow{CB}$+$\frac{3}{2}$$\overrightarrow{AB}$$•\overrightarrow{CB}$=$0+\frac{3}{2}$×3=$\frac{9}{2}$
故答案为:$\frac{9}{2}$
点评 本题考查了平面向量的几何运算,数量积,结合结合图形分解向量,属于中档题,关键是转化为容易计算的向量.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案| A. | {1,2,3,4,5,6} | B. | {1,2,3,4,5} | C. | {1,2,5} | D. | {1,2} |
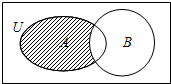
| A. | ∅ | B. | {0,1} | C. | (0,2) | D. | (-∞,2) |
| A. | ±5 | B. | ±4 | C. | $±\sqrt{5}$ | D. | ±2 |
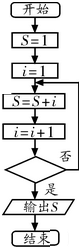
| A. | i>5 | B. | i>6 | C. | i>7 | D. | i>8 |
 如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A是切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点F.
如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A是切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点F.