题目内容
12.已知0<x1<x2<x3,a=$\frac{{{{log}_2}(2{x_1}+2)}}{x_1},b=\frac{{{{log}_2}(2{x_2}+2)}}{x_2},c=\frac{{{{log}_2}(2{x_3}+2)}}{x_3}$,则a、b、c的大小关系为( )| A. | c<a<b | B. | b<a<c | C. | a<b<c | D. | c<b<a |
分析 令f(x)=log2(2x+2),构造新函数g(x)=$\frac{f(x)}{x}$,数形结合判断函数g(x)的单调性,最后利用单调性比较大小即可.
解答 解:令f(x)=log2(2x+2),
令g(x)=$\frac{f(x)}{x}$,其几何意义为f(x)图象上的点(x,f(x))与原点(0,0)连线的斜率
由图可知函数g(x)为(-1,+∞)上的减函数
∵0<x1<x2<x3,
∴g(x1)>g(x2)>g(x3),
即a>b>c,
故选:D
点评 本题考查了对数函数的图象,数形结合判断函数单调性的方法,利用单调性比较大小,转化化归的思想方法

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.设x,y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≥2}\\{x≤2}\end{array}\right.$,则z=2x+y+1的最大值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
20.已知定义在R的函数f(x)满足:
①f(-x)=f(x);
②f(x-2)=f(x);
③?x1,x2∈[0,1](x1≠x2),$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$>0.
则( )
①f(-x)=f(x);
②f(x-2)=f(x);
③?x1,x2∈[0,1](x1≠x2),$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$>0.
则( )
| A. | 函数f(x)的图象关于直线x=$\frac{1}{2}$对称 | |
| B. | 函数f(x)的图象关关于点($\frac{1}{2}$,0)对称 | |
| C. | 函数f(x+1)在区间[2013,2014]内单调递增 | |
| D. | 函数f(x+1)的最小正周期为1 |
17.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若$\overrightarrow{PF}$=3$\overrightarrow{QF}$,则|QF|=( )
| A. | $\frac{5}{2}$ | B. | $\frac{8}{3}$ | C. | 3 | D. | 6 |
4.执行如图所示的程序框图,若输出实数k的值为4,则框图中x的值是( )


| A. | 4 | B. | 16 | C. | 24 | D. | 120 |
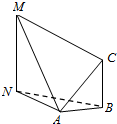 如图,为测量山高MN,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°已知山高BC=200m,则山高MN=300m.
如图,为测量山高MN,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°已知山高BC=200m,则山高MN=300m.