题目内容
17.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若$\overrightarrow{PF}$=3$\overrightarrow{QF}$,则|QF|=( )| A. | $\frac{5}{2}$ | B. | $\frac{8}{3}$ | C. | 3 | D. | 6 |
分析 通过抛物线的图象,利用抛物线的定义以及$\overrightarrow{PF}$=3$\overrightarrow{QF}$,求解即可.
解答 解:如下图所示,抛物线C':B的焦点为(2,0),准线为x=-2,准线与x轴的交点为N,P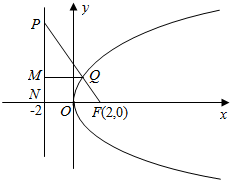
过点Q作准线的垂线,垂足为M,由抛物线的定义知:|MQ|=|QF|,
又因为$\overrightarrow{PF}$=3$\overrightarrow{QF}$,所以,3|MQ|=|PF|,
所以,$\frac{|MQ|}{|NF|}=\frac{|PQ|}{|PF|}$,可得:|MQ|=4×$\frac{2}{3}$=$\frac{8}{3}$.
所以,$|{QF}|=|{QM}|=\frac{8}{3}$.
故选:B.
点评 本题考查抛物线的简单性质的应用,抛物线的定义的应用,考查计算能力以及转化思想的应用.

练习册系列答案
相关题目
7.已知四面体ABCD的所有顶点都在球O的球面上,球O的半径为2,AB,AC,AD两两垂直,AB=$\sqrt{2}$,则四面体ABCD体积的最大值为( )
| A. | $\frac{7\sqrt{2}}{6}$ | B. | $\frac{7}{3}$ | C. | 2$\sqrt{2}$ | D. | 2 |
5.在复平面内,复数$\frac{2i}{1-i}$对应的点的坐标是( )
| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
12.已知0<x1<x2<x3,a=$\frac{{{{log}_2}(2{x_1}+2)}}{x_1},b=\frac{{{{log}_2}(2{x_2}+2)}}{x_2},c=\frac{{{{log}_2}(2{x_3}+2)}}{x_3}$,则a、b、c的大小关系为( )
| A. | c<a<b | B. | b<a<c | C. | a<b<c | D. | c<b<a |
2.设p,q是两个命题,则“p,q均为假命题”是“p∧q为假命题”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充分必要 | D. | 既不充分也不必要 |
9.已知函数f(x)=$\left\{\begin{array}{l}2lnx-x,x∈(0,2]\\ f(x-2),x∈(2,+∞)\end{array}$,a=log3162,b=$\frac{lg10000}{{{{log}_2}3}}$,则以下结论正确的是( )
| A. | f(a)<f(b)<0 | B. | f(b)<f(a)<0 | C. | 0<f(a)<f(b) | D. | 0<f(b)<f(a) |