题目内容
13．某校对数学、物理两科进行学业水平考前辅导，辅导后进行测试，按成绩（满分100分）划分为合格（成绩大于或等于70分）和不合格（成绩小于70分）．现随机抽取两科各100名学生的成绩统计如下：| 成绩（单位：分） | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
（2）数学合格一人可以赢得4小时机器人操作时间，不合格一人则减少1小时机器人操作
时间；物理合格一人可赢得5小时机器人操作时间，不合格一人则减少2小时机器人操作时间．在（1）的前提下，
（i）记X为数学一人和物理一人所赢得的机器人操作时间（单位：小时）总和，求随机变量X 的分布列和数学期望；
（ii）随机抽取5名学生，求这5名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于14小时的概率．
分析 （Ⅰ）结合所给的表格，把数学合格的人数除以100，可得数学合格的概率，把物理合格的人数除以100，可得物理合格的概率．
（Ⅱ）（ⅰ）随机变量X的所有取值为9，4，2，-3，求出相应的概率，可得随机变量X的分布列和数学期望；
（ii）根据抽查5位同学物理成绩所赢得的机器人操作时间不少于14个，求出抽查5位同学物理分数，合格人数，即可求抽查5位同学物理成绩所赢得的机器人操作时间不少于14个的概率．
解答 解：（Ⅰ）结合所给的表格可得数学合格的概率约为$\frac{40+32+8}{100}=\frac{4}{5}$，物理合格的概率约为$\frac{40+29+6}{100}=\frac{3}{4}$．
（Ⅱ）（ⅰ）随机变量X的所有取值为9，4，2，-3．则P（X=9）=$\frac{4}{5}×\frac{3}{4}=\frac{3}{5}$；P（X=4）=$\frac{1}{5}×\frac{3}{4}=\frac{3}{20}$；P（X=2）=$\frac{4}{5}×\frac{1}{4}=\frac{1}{5}$；P（X=-3）=$\frac{1}{5}×\frac{1}{4}=\frac{1}{20}$
所以，随机变量X的分布列为：
| X | 9 | 4 | 2 | -3 |
| P | $\frac{3}{5}$ | $\frac{3}{20}$ | $\frac{1}{5}$ | $\frac{1}{20}$ |
（ⅱ）抽查5位同学物理分数，合格n人，则不合格有5-n人，
依题意，得5n-2（5-n）≥14，解得n≥$\frac{24}{7}$所以n=4或n=5．
设“抽查5位同学物理考前辅导后进行的测试所赢得的机器人操作时间不少于14小时为事件A，则P（A）=${C}_{5}^{4}（\frac{3}{4}）^{4}×\frac{1}{4}+（\frac{3}{4}）^{5}=\frac{81}{128}$
点评 本题主要考查求离散型随机变量的分布列，古典概率及其计算公式，属于中档题．
练习册系列答案
相关题目
3．执行如图程序框图，若输出的S值为62，则判断框内为（ ）
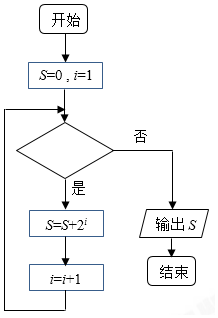
| A． | i≤4？ | B． | i≤5？ | C． | i≤6？ | D． | i≤7？ |
4．设{an}是等比数列，则对任何n∈N*，都有$\frac{1}{{{a_1}{a_2}}}•\frac{1}{{{a_2}{a_3}}}…\frac{1}{{{a_n}{a_{n+1}}}}$=（ ）
| A． | $\frac{1}{{{{（{a_1}•{a_n}）}^n}}}$ | B． | $\frac{1}{{{{（{a_1}•{a_{n+1}}）}^n}}}$ | C． | $\frac{1}{{{{（{a_1}•{a_n}）}^{n+1}}}}$ | D． | $\frac{1}{{{{（{a_1}•{a_{n+1}}）}^{n+1}}}}$ |
2．已知i是虚数单位，则i3+$\frac{1}{i}$=（ ）
| A． | -2i | B． | 2i | C． | -i | D． | i |