12.设F1、F2分别是椭圆$\frac{x^2}{4}$+y2=1的左、右焦点,若Q是该椭圆上的一个动点,则$\overrightarrow{Q{F_1}}$•$\overrightarrow{Q{F_2}}$的最大值和最小值分别为( )
| A. | 1与-2 | B. | 2与-2 | C. | 1与-1 | D. | 2与-1 |
11.椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,点M在椭圆上,且MF1⊥F1F2,|MF1|=$\frac{4}{3}$,|MF2|=$\frac{14}{3}$,则离心率e等于( )
| A. | $\frac{{\sqrt{5}}}{8}$ | B. | $\frac{{\sqrt{5}}}{6}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | $\frac{{\sqrt{5}}}{4}$ |
8.求满足下列条件的椭圆方程:
(1)长轴在x轴上,长轴长等于12,离心率等于$\frac{2}{3}$;
(2)椭圆经过点(-6,0)和(0,8);
(3)椭圆的一个焦点到长轴两端点的距离分别为10和4.
(1)长轴在x轴上,长轴长等于12,离心率等于$\frac{2}{3}$;
(2)椭圆经过点(-6,0)和(0,8);
(3)椭圆的一个焦点到长轴两端点的距离分别为10和4.
7.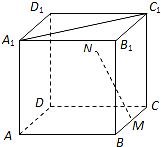 如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
 如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )| A. | 线段 | B. | 圆的一部分 | C. | 椭圆的一部分 | D. | 双曲线的一部分 |
6.点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个命题:
①三棱锥A1-D1DP的体积不变;
②A1P∥平面ACD1;
③DP⊥BC1;
④平面A1PB⊥平面PDB1.
其中正确的命题的序号是( )
①三棱锥A1-D1DP的体积不变;
②A1P∥平面ACD1;
③DP⊥BC1;
④平面A1PB⊥平面PDB1.
其中正确的命题的序号是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
5.正四面体ABCD中,M,N分别是棱BC和棱AC的中点,则异面直线AM和DN所成的角的余弦值为( )
0 246620 246628 246634 246638 246644 246646 246650 246656 246658 246664 246670 246674 246676 246680 246686 246688 246694 246698 246700 246704 246706 246710 246712 246714 246715 246716 246718 246719 246720 246722 246724 246728 246730 246734 246736 246740 246746 246748 246754 246758 246760 246764 246770 246776 246778 246784 246788 246790 246796 246800 246806 246814 266669
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | 0 |