Question

7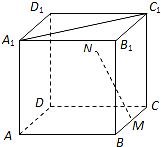．如图，在正方体中ABCD-A₁B₁C₁D₁，M为BC的中点，点N在四边形CDD₁C₁及其内部运动．若MN⊥A₁C₁，则N点的轨迹为（　　）

• A． 线段
• B． 圆的一部分
• C． 椭圆的一部分
• D． 双曲线的一部分

Answer 1

分析 正方体中ABCD-A₁B₁C₁D₁中，M为BC的中点，点N在四边形CDD₁C₁及其内部运动，
取CD、C₁D₁的中点Q、P，连接PQ，得出点N在线段PQ上时，MN⊥A₁C₁，说明原因即可．

解答 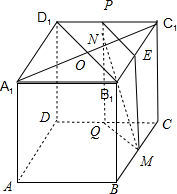解：正方体中ABCD-A₁B₁C₁D₁中，M为BC的中点，点N在四边形CDD₁C₁及其内部运动；
如图所示，
取CD、C₁D₁的中点Q、P，连接PQ，
当点N在线段PQ上时，MN⊥A₁C₁；
因为正方体ABCD-A₁B₁C₁D₁中，
连接B₁D₁，交A₁C₁于点O，∴B₁D₁⊥A₁D₁，
取B₁C₁的中点E，连接PE，则PE∥B₁D₁，
∴PE⊥A₁C₁；
又CC₁⊥平面A₁B₁C₁D₁，PQ∥CC₁，
∴PQ⊥平面A₁B₁C₁D₁，
∵A₁C₁?平面A₁B₁C₁D₁，
∴PQ⊥A₁C₁；
且PQ∩PE=P，
∴A₁C₁⊥平面PQME，
PQ?平面PQME，
∴A₁C₁⊥PQ；
∴N点的轨迹为线段PQ．
故选：A．

点评 本题以正方体为载体，考查了空间中的平行与垂直关系的应用问题，也考查了空间想象能力与逻辑思维能力的应用问题，是基础题目．