题目内容
11．椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点F1，F2，点M在椭圆上，且MF1⊥F1F2，|MF1|=$\frac{4}{3}$，|MF2|=$\frac{14}{3}$，则离心率e等于（ ）| A． | $\frac{{\sqrt{5}}}{8}$ | B． | $\frac{{\sqrt{5}}}{6}$ | C． | $\frac{{\sqrt{5}}}{3}$ | D． | $\frac{{\sqrt{5}}}{4}$ |
分析 由题意，|F1F2|=$\sqrt{（\frac{14}{3}）^{2}-（\frac{4}{3}）^{2}}$=2$\sqrt{5}$=2c，2a=$\frac{4}{3}$+$\frac{14}{3}$=6，即可求出椭圆的离心率．
解答 解：由题意，|F1F2|=$\sqrt{（\frac{14}{3}）^{2}-（\frac{4}{3}）^{2}}$=2$\sqrt{5}$=2c，2a=$\frac{4}{3}$+$\frac{14}{3}$=6，
∴e=$\frac{c}{a}$=$\frac{\sqrt{5}}{3}$．
故选：C．
点评 本题考查椭圆的定义，考查椭圆的几何性质，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
13．cos80°cos130°-sin80°sin130°等于（ ）
| A． | -$\frac{{\sqrt{3}}}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
6．点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动，则下列四个命题：
①三棱锥A1-D1DP的体积不变；
②A1P∥平面ACD1；
③DP⊥BC1；
④平面A1PB⊥平面PDB1．
其中正确的命题的序号是（ ）
①三棱锥A1-D1DP的体积不变；
②A1P∥平面ACD1；
③DP⊥BC1；
④平面A1PB⊥平面PDB1．
其中正确的命题的序号是（ ）
| A． | ①②③ | B． | ①②④ | C． | ①③④ | D． | ②③④ |
3．方程lgx-4+x=0的根一定位于区间（ ）
| A． | （5，6） | B． | （3，4） | C． | （2，3） | D． | （1，2） |
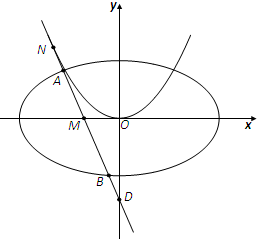椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，且以原点为圆心，椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切．