3.当双曲线C不是等轴双曲线时,我们把以双曲线C的实轴、虚轴的端点作为顶点的椭圆称为双曲线C的“伴生椭圆”.则离心率为$\sqrt{3}$的双曲线的“伴生椭圆”的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
20.已知中心在原点的椭圆与双曲线有公共焦点,左右焦点分别为F1,F2,且两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=10,椭圆与双曲线的离心率分别为e1,e2,则e2-e1的取值范围是( )
| A. | ($\frac{2}{3}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,$\frac{4}{3}$) |
19.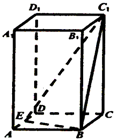 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
0 246547 246555 246561 246565 246571 246573 246577 246583 246585 246591 246597 246601 246603 246607 246613 246615 246621 246625 246627 246631 246633 246637 246639 246641 246642 246643 246645 246646 246647 246649 246651 246655 246657 246661 246663 246667 246673 246675 246681 246685 246687 246691 246697 246703 246705 246711 246715 246717 246723 246727 246733 246741 266669
 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )| A. | $\frac{8}{3}$ | B. | 4 | C. | $\frac{4}{3}$ | D. | 8 |
 如图,在四棱锥C-A1ABB1中,A1A∥BB1,A1A⊥平面ABC,∠ACB=$\frac{π}{2}$,AC=AA1=1,BC=BB1=2.
如图,在四棱锥C-A1ABB1中,A1A∥BB1,A1A⊥平面ABC,∠ACB=$\frac{π}{2}$,AC=AA1=1,BC=BB1=2.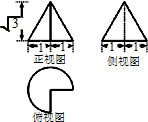 已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.
已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.