题目内容
2.平面上三个力$\overrightarrow{{F}_{1}}$、$\overrightarrow{{F}_{2}}$、$\overrightarrow{{F}_{3}}$作用于一点且处于平衡状态,|$\overrightarrow{{F}_{1}}$|=1(N),|$\overrightarrow{{F}_{2}}$|=$\frac{\sqrt{6}+\sqrt{2}}{2}$(N),$\overrightarrow{{F}_{1}}$与$\overrightarrow{{F}_{2}}$的夹角为45°,将$\overrightarrow{{F}_{1}}$的起点放在原点,终点在x轴的正半轴,$\overrightarrow{{F}_{2}}$的终点放在第一象限内.(1)$\overrightarrow{{F}_{3}}$的大小;
(2)求$\overrightarrow{{F}_{1}}$与$\overrightarrow{{F}_{3}}$的夹角大小.
分析 (1)三个力平衡则三个力的和为$\overrightarrow{0}$,移项,利用向量模的平方等于向量的平方求出向量的大小.
(2)利用三角形的余弦定理求出两个向量的夹角大小.
解答 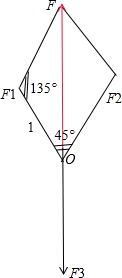 解:(1)如图,设力$\overrightarrow{{F}_{1}}$、$\overrightarrow{{F}_{2}}$的合力为$\overrightarrow{F}$,则|$\overrightarrow{F}$|=|$\overrightarrow{{F}_{3}}$|,
解:(1)如图,设力$\overrightarrow{{F}_{1}}$、$\overrightarrow{{F}_{2}}$的合力为$\overrightarrow{F}$,则|$\overrightarrow{F}$|=|$\overrightarrow{{F}_{3}}$|,
∵∠F1OF2=45°,∴∠OF1F=135°.
在△OF1F中,由余弦定理得${\overrightarrow{OF}}^{2}$=${\overrightarrow{{OF}_{1}}}^{2}$+${\overrightarrow{{OF}_{2}}}^{2}$-2|$\overrightarrow{{OF}_{1}}$|•|$\overrightarrow{{OF}_{2}}$|•cos135°
=1+${(\frac{\sqrt{6}+\sqrt{2}}{2})}^{2}$-2×1×$\frac{\sqrt{6}+\sqrt{2}}{2}$×(-$\frac{\sqrt{2}}{2}$)=4+2$\sqrt{3}$=${(\sqrt{3}+1)}^{2}$,
∴|$\overrightarrow{OF}$|=$\sqrt{3}$+1,即|$\overrightarrow{{F}_{3}}$|=1+$\sqrt{3}$.
(2)依题意,由正弦定理得sin∠F1OF=$\frac{|\overrightarrow{{FF}_{1}}|•sin∠{FF}_{1}O}{|\overrightarrow{OF}|}$=$\frac{1}{2}$,
∴∠F1OF=30°,从而$\overrightarrow{{F}_{1}}$与$\overrightarrow{{F}_{3}}$的夹角为150°.
综上可得,$\overrightarrow{{F}_{3}}$的大小为(1+3)N,$\overrightarrow{{F}_{3}}$与 $\overrightarrow{{F}_{1}}$的夹角为150°.
点评 本题考查向量模的性质:向量模的平方等于向量的平方、考查三角形的余弦定理,属于中档题.

 作业辅导系列答案
作业辅导系列答案| A. | m≥1 | B. | m≥1或0<m<1 | C. | m≥1且m≠5 | D. | 0<m<5且m≠1 |
| A. | $±\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
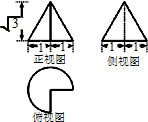 已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.
已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.