题目内容
19.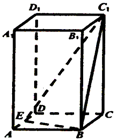 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )| A. | $\frac{8}{3}$ | B. | 4 | C. | $\frac{4}{3}$ | D. | 8 |
分析 利用已知条件求出棱锥的底面面积与高,即可求出结果.
解答 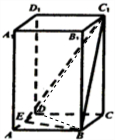 解:如图连结DB,DC1,正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,棱锥的底面面积为:$\frac{1}{2}×1×2$=1,棱锥的高为CC1=4,
解:如图连结DB,DC1,正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,棱锥的底面面积为:$\frac{1}{2}×1×2$=1,棱锥的高为CC1=4,
所求棱锥的体积为:$\frac{1}{3}×1×4$=$\frac{4}{3}$.
故选:C.
点评 本题考查棱锥的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
1.在△ABC中,sin2A=sinBsinC,∠A=$\frac{π}{3}$,则∠B等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
8.已知集合A={x|log3(x2-2x)>1},B={x∈N|x<5},则( )
| A. | A∩B=(3,5) | B. | A∪B=5 | C. | A∪B={x|x≤5} | D. | A∩B={4} |
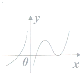
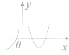
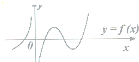 已知函数y=f(x)在定义域内可导,且图象如图所示,则此导函数y=f′(x)的图象可知为图中的( )
已知函数y=f(x)在定义域内可导,且图象如图所示,则此导函数y=f′(x)的图象可知为图中的( )