��Ŀ����
5����֪��ԲG��$\frac{x^2}{a^2}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{{\sqrt{6}}}{3}$���ҽ���Ϊ��2$\sqrt{2}$��0������ԭ��O��ֱ��l����Բ��A��B���㣬�߶�AB�Ĵ�ֱƽ���߽���ԲG�ڵ�M����������ԲG�ķ��̣�
������֤��$\frac{1}{{{{|{OA}|}^2}}}$+$\frac{1}{{{{|{OM}|}^2}}}$Ϊ��ֵ�������AOM�������Сֵ��
���� ��I��������$c=2\sqrt{2}$��$e=\frac{c}{a}=\frac{{\sqrt{6}}}{3}$����b2=a2-c2������������ɣ�
��II����ֱ��l��б�ʷ������ۣ���1��������ʱֱ���������2����ֱ��l���������ֱʱ����ֱ��l�ķ���Ϊy=kx��k��0����A��x1��y1��������Բ����������Ϊ��1+3k2��x2=12�����ɵó�|OA|2����OM���߶�AB�Ĵ�ֱƽ���ߣ��ʷ���Ϊ$y=-\frac{1}{k}x$��ͬ���ɵ�|OM|2������$\frac{1}{{{{|{OA}|}^2}}}$+$\frac{1}{{{{|{OM}|}^2}}}$����֤��Ϊ��ֵ��
���AOM���ʱ���������ַ���������һ����$\frac{1}{3}=\frac{1}{{{{|{OA}|}^2}}}+\frac{1}{{{{|{OM}|}^2}}}��\frac{2}{{|{OA}|•|{OM}|}}$�����ɵó�������������AOM�����$S=\frac{1}{2}|{OA}|•|{OM}|$���ѣ�2�����뻯�����û�������ʽ�����ʼ��ɵó���
��� ��I���⣺������$c=2\sqrt{2}$��
��$e=\frac{c}{a}=\frac{{\sqrt{6}}}{3}$����$a=2\sqrt{3}$��
��b2=a2-c2=4
����ԲG�ķ���Ϊ$\frac{x^2}{12}+\frac{y^2}{4}=1$��
����֤������1����ֱ��l��ֱ��������ʱ��
��$\frac{1}{{{{|{OA}|}^2}}}+\frac{1}{{{{|{OM}|}^2}}}=\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{3}$��
��AOM�����$S=\frac{1}{2}|{OA}|•|{OM}|=2\sqrt{3}$��
��2����ֱ��l���������ֱʱ����ֱ��l�ķ���Ϊy=kx��k��0����A��x1��y1����
��$\left\{\begin{array}{l}y=kx\\ \frac{x^2}{12}+\frac{y^2}{4}=1\end{array}\right.$��Ԫ�ã�1+3k2��x2=12��
��${x_1}^2=\frac{12}{{1+3{k^2}}}$��${y_1}^2={k^2}{x_1}^2=\frac{{12{k^2}}}{{1+3{k^2}}}$��
��${|{OA}|^2}={x_1}^2+{y_1}^2=\frac{{12��1+{k^2}��}}{{1+3{k^2}}}$��
��OM���߶�AB�Ĵ�ֱƽ���ߣ��ʷ���Ϊ$y=-\frac{1}{k}x$��
ͬ���ɵ�${|{OM}|^2}=\frac{{12��1+{k^2}��}}{{{k^2}+3}}$��
�Ӷ�$\frac{1}{{{{|{OA}|}^2}}}+\frac{1}{{{{|{OM}|}^2}}}=\frac{{1+3{k^2}}}{{12��1+{k^2}��}}+\frac{{{k^2}+3}}{{12��1+{k^2}��}}=\frac{{4{k^2}+4}}{{12��1+{k^2}��}}=\frac{1}{3}$Ϊ��ֵ��
����һ����$\frac{1}{3}=\frac{1}{{{{|{OA}|}^2}}}+\frac{1}{{{{|{OM}|}^2}}}��\frac{2}{{|{OA}|•|{OM}|}}$������|OA|•|OM|��6��
���ҽ���|OA|=|OM|ʱ����1+3k2=k2+3��k=��1ʱ���Ⱥų�����
���AOM�����$S=\frac{1}{2}|{OA}|•|{OM}|��3$��
�൱k=��1ʱ����AOM���������Сֵ3��
����������AOM�����$S=\frac{1}{2}|{OA}|•|{OM}|$��
��${S^2}=\frac{1}{4}{|{OA}|^2}•{|{OM}|^2}=\frac{1}{4}��\frac{{12��1+{k^2}��}}{{1+3{k^2}}}��\frac{{12��1+{k^2}��}}{{{k^2}+3}}$=$\frac{{36{{��1+{k^2}��}^2}}}{{��1+3{k^2}����{k^2}+3��}}��\frac{{36{{��1+{k^2}��}^2}}}{{{{��\frac{{1+3{k^2}+{k^2}+3}}{2}��}^2}}}$=9��
�൱�ҽ���1+3k2=k2+3ʱ����k=��1ʱ����AOM���������Сֵ3��
���� ���⿼����Բ���ߵı����̼������ʡ�ֱ������Բ�ཻ����ת��Ϊ������������ϵ���Ĺ�ϵ��������������㹫ʽ����������ʽ�����ʡ����ֱ��ֱ��б��֮��Ĺ�ϵ�Ȼ���֪ʶ��������ܣ���������������������������������⣮

| A�� | p1=p2 | B�� | p1+p2=1 | C�� | p1��p2 | D�� | p1��p2 |
| A�� | $\sqrt{2}$ | B�� | 2 | C�� | 2$\sqrt{2}$ | D�� | 4 |
| A�� | ��$\frac{2}{3}$��+�ޣ� | B�� | ��$\frac{4}{3}$��+�ޣ� | C�� | ��0��$\frac{2}{3}$�� | D�� | ��$\frac{2}{3}$��$\frac{4}{3}$�� |
| A�� | y=$\sqrt{3}x+3\sqrt{3}$+2 | B�� | y=$\frac{{\sqrt{3}}}{3}x+\sqrt{3}$+2 | C�� | y=$\sqrt{3}x-3\sqrt{3}$-2 | D�� | y=$\frac{{\sqrt{3}}}{3}x-\sqrt{3}$-2 |
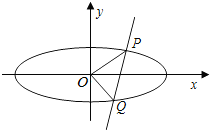 ��֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0����������Ϊ$\frac{{\sqrt{3}}}{2}$������ԲC�����㣨0��1����
��֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0����������Ϊ$\frac{{\sqrt{3}}}{2}$������ԲC�����㣨0��1����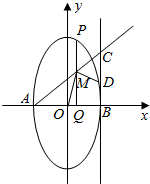 ��֪��Բ$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1��a��b��0����������e=$\frac{{\sqrt{3}}}{2}$����Բ���Ҷ���ֱ�ΪA��B����A����Բ������ľ���֮��Ϊ4����PΪ��Բ�ϲ�ͬ��A��B����һ�㣬��PQ��x�ᣬQΪ���㣮MΪ�߶�PQ�е㣬ֱ��AM��ֱ��l��x=b�ڵ�C��DΪ�߶�BC�е㣨��ͼ����
��֪��Բ$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1��a��b��0����������e=$\frac{{\sqrt{3}}}{2}$����Բ���Ҷ���ֱ�ΪA��B����A����Բ������ľ���֮��Ϊ4����PΪ��Բ�ϲ�ͬ��A��B����һ�㣬��PQ��x�ᣬQΪ���㣮MΪ�߶�PQ�е㣬ֱ��AM��ֱ��l��x=b�ڵ�C��DΪ�߶�BC�е㣨��ͼ����