题目内容
8. 如图,在四棱锥C-A1ABB1中,A1A∥BB1,A1A⊥平面ABC,∠ACB=$\frac{π}{2}$,AC=AA1=1,BC=BB1=2.
如图,在四棱锥C-A1ABB1中,A1A∥BB1,A1A⊥平面ABC,∠ACB=$\frac{π}{2}$,AC=AA1=1,BC=BB1=2.(1)求证:平面A1AC⊥平面B1BC;
(2)若点C在棱AB上的射影为点P,求二面角A1-PC-B1的余弦值.
分析 (1)证明BC⊥平面A1AC,即可证明平面A1AC⊥平面B1BC;
(2)证明∠A1PB1即二面角的A1-PC-B1一个平面角,利用tan∠A1PB1=-tan(∠A1PA+∠B1PB),即可求二面角A1-PC-B1的余弦值.
解答 (1)证明:因为A1A⊥平面ABC,所以A1A⊥BC,…(2分)
又因为AC⊥BC,A1A∩AC=A,
所以BC⊥平面A1AC,…(4分)
所以平面A1AC⊥平面B1BC.…(5分)
(2)解:先考查二面角A-PC-A1和二面角B-PC-B1,
因为A1A⊥平面ABC,所以A1A⊥CP,
又因为CP⊥AB,
所以CP⊥面A1ABB1,所以CP⊥A1P,CP⊥B1P,
所以∠A1PB1即二面角的A1-PC-B1一个平面角,…(7分)
因为tan∠A1PA=$\frac{A{A}_{1}}{AP}$=$\sqrt{5}$,…(9分)
tan∠B1PB=$\frac{B{B}_{1}}{BP}$=$\frac{\sqrt{5}}{2}$,…(11分)
所以tan∠A1PB1=-tan(∠A1PA+∠B1PB)=-$\frac{\sqrt{5}+\frac{\sqrt{5}}{2}}{1-\sqrt{5}•\frac{\sqrt{5}}{2}}$=$\sqrt{5}$,…(14分)
所以cos∠A1PB1=$\frac{\sqrt{6}}{6}$,
所以二面角A1-PC-B1的余弦值为$\frac{\sqrt{6}}{6}$.…(15分)
点评 本题考查平面与平面垂直的判定,考查线面垂直的判定与性质,考查二面角的平面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列关于随机抽样的说法不正确的是( )
| A. | 简单随机抽样是一种逐个抽取不放回的抽样 | |
| B. | 系统抽样和分层抽样中每个个体被抽到的概率都相等 | |
| C. | 有2006个零件,先用随机数表法剔除6个,再用系统抽样方法抽取20个作为样本,每个零件入选样本的概率都为$\frac{1}{100}$ | |
| D. | 当总体是由差异明显的几个部分组成时适宜采取分层抽样 |
3.当双曲线C不是等轴双曲线时,我们把以双曲线C的实轴、虚轴的端点作为顶点的椭圆称为双曲线C的“伴生椭圆”.则离心率为$\sqrt{3}$的双曲线的“伴生椭圆”的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
13.过点M(-1,1)作斜率为$\frac{1}{2}$的直线与椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)相交于A,B两点,若M是线段AB的中点,则椭圆C的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
18.函数y=f(x)的图象如图所示,则以下描述正确的是( )
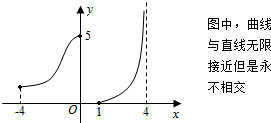

| A. | 函数f(x)的定义域为[-4,4) | |
| B. | 函数f(x)的值域为[0,5] | |
| C. | 此函数在定义域内既不是增函数也不是减函数 | |
| D. | 对于任意的y∈[0,+∞),都有唯一的自变量x与之对应 |