题目内容
20.已知中心在原点的椭圆与双曲线有公共焦点,左右焦点分别为F1,F2,且两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=10,椭圆与双曲线的离心率分别为e1,e2,则e2-e1的取值范围是( )| A. | ($\frac{2}{3}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,$\frac{4}{3}$) |
分析 设椭圆与双曲线的半焦距为c,PF1=r1,PF2=r2.利用三角形中边之间的关系得出c的取值范围,再根据椭圆或双曲线的性质求出各自的离心率,最后依据c的范围即可求出e2-e1的取值范围.
解答 解:设椭圆与双曲线的半焦距为c,|PF1|=r1,|PF2|=r2.
由题意知r1=10,r2=2c,且r1>r2,2r2>r1,
∴2c<10,2c+2c>10,
∴2.5<c<5,
∴e1=$\frac{2c}{10-2c}$=$\frac{c}{5-c}$;e2=$\frac{2c}{10+2c}$=$\frac{c}{5+c}$.
∴e2-e1=$\frac{c}{5-c}$-$\frac{c}{5+c}$=$\frac{2{c}^{2}}{25-{c}^{2}}$=$\frac{2}{\frac{25}{{c}^{2}}-1}$>$\frac{2}{3}$,
故选:A.
点评 本小题主要考查函数单调性的应用、椭圆的简单性质、双曲线的简单性质、不等式的性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
12.已知抛物线y=$\frac{1}{2}$x2的焦点与椭圆$\frac{y^2}{m}$+$\frac{x^2}{2}$=1的一个焦点重合,则m=( )
| A. | $\frac{7}{4}$ | B. | $\frac{127}{64}$ | C. | $\frac{9}{4}$ | D. | $\frac{129}{64}$ |
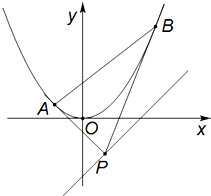 已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,
已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,