题目内容
7．
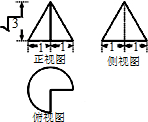已知某几何体的三视图如图所示，则该几何体的体积为$\frac{\sqrt{3}π}{4}$；表面积为$\frac{9π}{4}+\sqrt{3}$．
分析 根据三视图可得几何体是圆锥，判断几何体的直观图，判断圆锥的底面半径以及高，代入圆锥体积，求解表面积．
解答 解：由题意可知：几何体是圆锥去掉$\frac{1}{4}$个圆锥，圆锥的底面半径为：1；高为：$\sqrt{3}$；
圆锥的母线为：2，
几何体的体积为：$\frac{3}{4}×\frac{1}{3}×{1}^{2}π×\sqrt{3}$=$\frac{\sqrt{3}π}{4}$．
几何体的表面积为：$\frac{3}{4}×{1}^{2}π$$+\frac{3}{4}×\frac{1}{2}×2π×2$$+2×\frac{1}{2}×1×\sqrt{3}$=$\frac{9π}{4}+\sqrt{3}$．
故答案为：$\frac{\sqrt{3}π}{4}$；$\frac{9π}{4}+\sqrt{3}$．
点评 本题考查了由三视图求几何体的表面积与体积，解答此类问题的关键是判断几何体的形状及数据所对应的几何量．
练习册系列答案
相关题目
8．
某企业员工共500人参加“学雷锋”志愿活动，按年龄分组：第一组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图所示．
（1）表是年龄的频数分布表，求正整数a，b的值；
（2）根据频率分布直方图，估算该企业员工的平均年龄及年龄的中位数；
（3）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．
某企业员工共500人参加“学雷锋”志愿活动，按年龄分组：第一组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图所示．| 区间 | [25，30） | [30，35） | [35，40） | [40，45） | [45，50] |
| 人数 | 50 | 50 | a | 150 | b |
（2）根据频率分布直方图，估算该企业员工的平均年龄及年龄的中位数；
（3）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．
12．已知抛物线y=$\frac{1}{2}$x2的焦点与椭圆$\frac{y^2}{m}$+$\frac{x^2}{2}$=1的一个焦点重合，则m=（ ）
| A． | $\frac{7}{4}$ | B． | $\frac{127}{64}$ | C． | $\frac{9}{4}$ | D． | $\frac{129}{64}$ |
16．四面体ABCD的外接球为O，AD⊥平面ABC，AD=2，△ABC为边长为3的正三角形，则球O的表面积为（ ）
| A． | 32π | B． | 16π | C． | 12π | D． | $\frac{32}{3}$π |
17．过点P（2，3），并且在两坐标轴上的截距相等的直线方程是（ ）
| A． | x-y+1=0 | B． | x-y+1=0或3x-2y=0 | ||
| C． | x+y-5=0 | D． | x+y-5=0或3x-2y=0 |